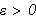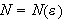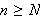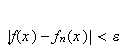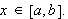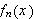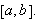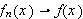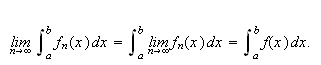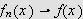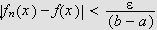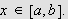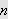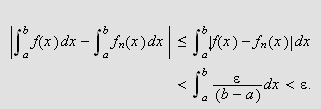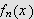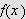PROBLEMENE
Som vi har sett førte Fouriers løsning av varmelikningen til at
matematikerne måtte tenke nytt, og det bar noen ganger galt avsted da
begrepsapparatet man på den tid var i besittelse av hverken var presist
nok eller generelt nok. For å sette Fouriers teorier litt i perspektiv
kan vi se på hvordan noen av begrepene man brukte da ble påvirket
nettopp på denne tiden, og - i noen tilfeller - av arbeidene hans.
Akkurat i hvor stor grad Fourier påvirket
utviklingen av analysen får vel være et åpent
spørsmål, men at det i hans kjølvann fulgte en presisering og
omarbeiding av flere begreper er utvilsomt. Vi kan altså ikke være
for strenge mot Fourier når han ikke hadde det samme begrepsapparatet som
vi har i dag. Hans arbeider i varmeteori ansees fortsatt som trendsettende for
vitenskaplig nøyaktighet. Fourier var først og fremst opptatt av
å gi en matematisk beskrivelse av naturen. Han var mindre interessert i
matematisk begrepsbygning og teori.
Det som er interessant er at problemstillingene for to hundre år siden er
noe av de samme som studenter ved høyere utdanning og elever ved
videregående skoler møter i dag. Både teoriene vedrørende
integrasjon og funksjoner så vel som konvergensbegrepet måtte
revideres. Disse begrepene er jo også problematiske for de som skal
læ re stoffet i dag. I dette kapitlet skal vi se på hvordan man
ryddet opp i noen av begrepene innen analysen. I et senere kapittel skal vi
også komme litt inn på hvordan dette kan relateres til
skolematematikken i våre dager.
I 1873 kom Du Bois-Reymond Note_1 med
et eksempel på en funksjon som var

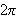 -periodisk
og kontinuerlig, og som hadde Fourierrekke som divergerte i et punkt [TWK,
s.67]. Men Fourier påsto jo at alle funksjoner
kunne representeres ved Fourierrekker som konvergerer mot funksjonen! Hvordan
skulle man da kunne ha en ''pen'' Fourierteori? Nå må vi tenke oss
til holdningen Fouriers samtid hadde til matematikk. Man skulle ha en
helhetlig vitenskap, og analysen skulle være generelt gyldig innenfor en
passende valgt klasse av funksjoner. Med slike funksjoner som Du Bois-Reymond
la fram, så det ut til at man måtte skreddersy funksjonsklasser
avhengig av hvilket problem man studerte. Dette var en
vanskelig tanke for to hundre år siden, og ble nok oppfattet som
matematisk fusk. Vi kan kanskje se for oss flere veier ut av uføret:
-periodisk
og kontinuerlig, og som hadde Fourierrekke som divergerte i et punkt [TWK,
s.67]. Men Fourier påsto jo at alle funksjoner
kunne representeres ved Fourierrekker som konvergerer mot funksjonen! Hvordan
skulle man da kunne ha en ''pen'' Fourierteori? Nå må vi tenke oss
til holdningen Fouriers samtid hadde til matematikk. Man skulle ha en
helhetlig vitenskap, og analysen skulle være generelt gyldig innenfor en
passende valgt klasse av funksjoner. Med slike funksjoner som Du Bois-Reymond
la fram, så det ut til at man måtte skreddersy funksjonsklasser
avhengig av hvilket problem man studerte. Dette var en
vanskelig tanke for to hundre år siden, og ble nok oppfattet som
matematisk fusk. Vi kan kanskje se for oss flere veier ut av uføret:
-
Funksjonsbegrepet kunne redefineres, slik at man kunne
finne en klasse funksjoner som var spesielt egnet innen Fourieranalyse, og der
man kunne ha ''pene'' resultater. Dette må vel likevel sies
å være en kunstig løsning av problemet.
-
En annen løsning ville være å oppdatere selve
konvergensbegrepet, altså ved å finne andre
måter rekker kan konvergere på. Slik kunne man kanskje snakke om en
spesiell klasse rekker som passet til problemet.
-
En tredje mulighet kunne være å finne andre
systemer som basis for utvikling i Fourierrekker, slik at
''skrekkeksempler'' som Du Bois-Reymond fant ikke skulle forekomme.
Alle disse remediene ble (selvfølgelig) undersøkt, og de utforskes
fortsatt. Vi skal i dette kapittelet se på den første muligheten,
det vil si ta for oss hvordan sentrale begreper som funksjon, konvergens og
integral ble endret på denne tiden. I kapittel 5 skal vi se
på hvordan Fejér brukte den andre utveien, nemlig ved å finne
en annen type konvergens. Den tredje utveien førte til en helt ny gren av
Fourieranalysen, såkalt Wavelets, som er et
veldig aktuelt område i dag.
Først tar vi en kikk på utviklingen av funksjonsbegrepet.
Funksjonsbegrepet
Man begynte å debattere funksjonsbegrepet allerede før Fourier kom
på banen. Et av problemene som førte til en slik diskusjon var
imidlertid ganske likt Fouriers varmeledningsproblem. Problemet med
den svingende strengen satte fart (og sinne) i
diskusjonen. Problemet var: hva er egentlig en
funksjon? Hvordan skulle man presist definere en funksjon? Det er ikke
tvil om at enkelte hadde sterke følelser rundt dette, og at debatten
varte over lang tid. Det ser vi klart fra et utsagn fra
Hermite Note_2 , som i et brev til
Stieltjes Note_3 skrev (1893):
''Jeg snur meg med frykt og avsky bort fra denne beklagelige farsotten av
funksjoner som ikke har noen derivert.''
Hvorfor er funksjonsbegrepet så viktig? En av grunnene kan være at
man i uminnelige tider har vært opptatt av hvordan ting endrer seg.
Spesielt har (og er) endring i tid noe man har forsøkt å utforske.
Hvordan månen (eller andre legemer) beveger seg på himmelen er
eksempel på det, så dette er altså funksjoner av tiden. Et
slikt funksjonsbegrep er imidlertid veldig filosofisk, og ikke presist nok i
en matematisk sammenheng.
Eulers funksjonsbegrep
Man sier gjerne at begrepet funksjon, som et
grunnbegrep i den matematiske analysen, fødtes ved innføringen av
Eulers funksjonsbegrep i 1755. Men selv om Euler kom med et funksjonsbegrep
som likner vår tids definisjon, var ikke den matematiske verden
på den tiden like flinke til å anvende Eulers begrep i praksis.
Først Dirichlet benyttet i praksis Eulers funksjonsbegrep.
Fra kurver til funksjoner
Helt opp til 1500-tallet hadde man en oppfatning av at algebra og geometri var
omtrent samme sak. I [TL1, s.211] nevnes eksemplet med at det som vi i dag ser
på som en andregradslikning ble sett på som en geometrioppgave med
kvadrater og rektangler. Likninga

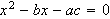 ble oppfattet som å finne ''det linjestykket
ble oppfattet som å finne ''det linjestykket

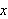 som er slik at arealet til et kvadrat med sider
som er slik at arealet til et kvadrat med sider

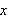 er lik summen av arealene av rektanglene med sider på henholdsvis
er lik summen av arealene av rektanglene med sider på henholdsvis

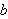 og
og

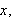 og
og

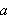 og
og

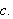 En slik sammenheng sporer vi helt tilbake til de gamle grekere. Denne
''geometriseringen'' gjorde kanskje sitt til at generelle funksjoner som ikke
var knyttet til en fysisk tolkning ikke var så mye brukt. Først med
inntoget til den analytiske geometrien begynte ting å likne på det
som vi kjenner til. Selv om Leibniz etterhvert kom med sin
infinitesimalregning, dreide det seg likefullt om kurver og arealer under
kurvene.
En slik sammenheng sporer vi helt tilbake til de gamle grekere. Denne
''geometriseringen'' gjorde kanskje sitt til at generelle funksjoner som ikke
var knyttet til en fysisk tolkning ikke var så mye brukt. Først med
inntoget til den analytiske geometrien begynte ting å likne på det
som vi kjenner til. Selv om Leibniz etterhvert kom med sin
infinitesimalregning, dreide det seg likefullt om kurver og arealer under
kurvene.
Etterhvert ble det gitt ut to arbeider med en ny vinkling.
Fermat Note_4 ga ut
Isagoge ad locos planos et solidos isagoge (Om likningene til
plan og faste legemer; 1679), og Descartes ga ut La
Géométrie (1637) som en utvidelse av hans hovedverk
Discourse de la méthode
Note_5 . I arbeidene til disse to
storhetene markeres overgangen til at man beskriver en kurve kun ved hjelp av
en likning eller utsagn av typen
''en sirkel med radius

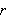 og sentrum i
og sentrum i

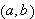 er de punkt
er de punkt

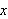 og
og

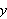 som tilfredsstiller
som tilfredsstiller
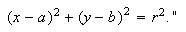
Fram til midten av 1700-tallet endret nå fokus seg gradvis fra kurver til
funksjoner.
To ankepunkter hos Euler
Euler skulle nå komme med sin funksjonsdefinisjon, og han kvitter seg med
kurvebegrepet i verkene Introductio in analysis infitorum
(1748) og Institutiones calculi differentialis
(1755). Her definerer han en funksjon slik:
''En funksjon av en variable størrelse er et analytisk uttrykk som
på en eller annen måte er sammensatt av denne variable
størrelsen og av tall eller konstante størrelser.'' ([JL, s.7],
[TL1, s.212])
Ideen til en slik definisjon hadde kommet fra Bernoulli (1718). Noen
ankepunkter har vi imidlertid til en slik definisjon:
-
Hva han mente med analytisk uttrykk er uklart. Kun ved
å se på Eulers praktiske bruk av funksjoner kan vi prøve
å forstå hva han mener.
Lebesgue Note_6 ga senere det vi i dag
bruker som definisjon av analytisk uttrykk.
fyll ut kanskjecomment
-
Variabel størrelse er et annet begrep fra
definisjonen som bør kommenteres. Her mener Euler at de variable skal
kunne anta alle komplekse verdier, og ikke benyttes
kun på et intervall. Igjen er det ønsket om den helhetlige analysen
som ligger bak. Denne tanken blir også gjerne kalt den
variables generalitet. Euler begrenset seg riktignok
til de reelle tallene enkelte ganger, men ytterligere skjerpinger ville han
nok ikke godtatt.
Innunder Eulers begrep havner forskjellige typer formler, som kunne være
sammensatt av endelig eller uendelig mange operasjoner. Vi skjønner at
det at han ikke skilte mellom divergente og konvergente rekker ville føre
til selvmotsigelser. Euler
så på
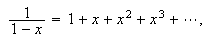
som vi nå vet kun holder for

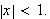 Euler ''definerte seg ut av problemet'' ved å si at summen til en rekke
er
Euler ''definerte seg ut av problemet'' ved å si at summen til en rekke
er
''det uttrykket som framkommer av rekkeutviklingen til en uendelig rekke.''
Flere var skeptiske til dette, blant andre d'Alembert (og senere Abel) mente
at man ikke kunne regne slik med rekker som ikke konvergerte. Ellers ble
også uttrykk som hadde flere

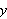 -verdier
tilhørende en og samme
-verdier
tilhørende en og samme

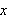 -verdi
inkludert av Eulers funksjonsbegrep. Funksjonslikhet ble også annerledes
enn hvordan vi ville ha forklart det i dag. For eksempel er to funksjoner like
hos Euler dersom han klarer å omforme den ene til den andre. Vi ville ha
sagt at to funksjoner
-verdi
inkludert av Eulers funksjonsbegrep. Funksjonslikhet ble også annerledes
enn hvordan vi ville ha forklart det i dag. For eksempel er to funksjoner like
hos Euler dersom han klarer å omforme den ene til den andre. Vi ville ha
sagt at to funksjoner

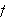 og
og

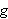 er like dersom de er definert på en felles definisjonsmengde og
er like dersom de er definert på en felles definisjonsmengde og

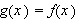 for alle
for alle

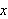 i definisjonsmengden.
i definisjonsmengden.
Man tilla på denne tiden funksjoner mange egenskaper som vi i dag ser
på som langt fra selvfølgelige. F.eks. at alle funksjoner kan
utvikles i en potensrekke. Euler skrev til og med at den faktiske utvikling av
en funksjon i potensrekker ville fjerne enhver tvil man måtte ha omkring
lovligheten av dette.
Fra kurve til funksjon og tilbake til kurve
Snart kom problemet med den svingende strengen i søkelyset, og
følgelig debatten om hvilke funksjoner man kunne tillate som
utgangsposisjoner for strengen (også omtalt i kapittel 1). Her hadde
d'Alembert funnet en løsning sammensatt av analytiske uttrykk. Han brukte
imidlertid Eulers første funksjonsbegrep. Euler mente dette begrenset
klassen av mulige utgangsposisjoner. Men siden odde utvidelser av
utgangsposisjonen inngår i løsningen mente Euler at slike odde
utvidelser av funksjoner også måtte komme innunder
funksjonsdefinisjonen. Ansporet av de fysiske mulighetene i problemet tillot
han vilkårlige kurver som utgangsposisjon og utvidet disse i en odde,
periodisk funksjon. Hans eget eksempel var en streng som ved

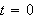 hadde form som en del av en sirkelperiferi. Euler sa at man finner
utgangsfunksjonen ved å gjøre denne periferien odde og periodisk, og
altså ikke følge den analytiske fortsettelsen (som Euler uttrykte
det), som er sirkelen.
hadde form som en del av en sirkelperiferi. Euler sa at man finner
utgangsfunksjonen ved å gjøre denne periferien odde og periodisk, og
altså ikke følge den analytiske fortsettelsen (som Euler uttrykte
det), som er sirkelen.
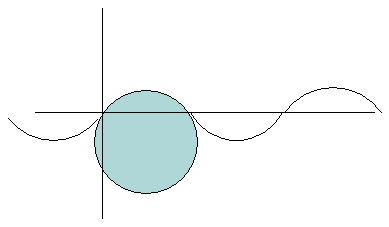
Forskjellen på analytisk
fortsettelse (sirkelen) og periodisk fortsettelse.
Euler gikk nå (ett år etter hans innføring av
funksjonsbegrepet) tilbake på sin egen definisjon og godtok
nå også delt forskrift. Dette ble gjort i arbeidet
De usu functionum discontinarium in analysi, og han
kalte disse diskontinuerlige funksjoner. Altså en helt annen betydning av
begrepet (dis-)kontinuerlig enn vi bruker i dag. I [JL] benyttes notasjonen
E-kontinuerlig for å skille Eulers oppfatning av
kontinuitet fra vår. Dette hadde selvfølgelig ingenting med
kontinuitet å gjøre, slik vi definerer det i dag. For eksempel er
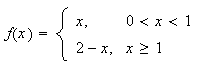
diskontinuerlig etter Eulers definisjon, men kontinuerlig etter dagens
definisjon. Euler kalte også funksjoner som var tegnet helt
på frihå nd, altså løsrevet fra et analytisk uttrykk, for
diskontinuerlige.
Nå hadde man altså før hatt et funksjonsbegrep som tilordner en
kurve til en funksjon, mens ringen nå ble sluttet ved at man fikk en
korrespondanse tilbake igjen. Altså at en vilkårlig kurve skulle
kunne betegne en (muligens E-diskontinuerlig) funksjon. Striden med d'Alembert
om strengen fortsatte. Nå mente d'Alembert rett og slett at det var fusk
å benytte slike utvidelser av utgangsposisjonen. Igjen ser vi at man
helst hadde ønsket seg at analysen hadde hatt de pene egenskapene man
fant innen de analytiske uttrykkene. En enda sterkere kritikk av Euler kom da
d'Alembert viste at de E-diskontinuerlige funksjonene ikke ville
tilfredsstille bølgelikningen der den andrederiverte hadde en
diskontinuitet. For eksempel har funksjonen

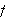 over et knekkpunkt og vil ikke være deriverbar der.
over et knekkpunkt og vil ikke være deriverbar der.
Eulers ''nådestøt'' fra Fourier
Etter at Fouriers bok om varmeteori hadde blitt utgitt i 1822, og Fouriers
teorier blitt mer kjent, fikk man flere indikasjoner på at Eulers
funksjonsbegrep ikke var tilstrekkelig. Her kom de mest konkrete eksemplene
på at definisjonene til Euler ikke var de mest fordelaktige. Fourier
hevdet at en like funksjon kan representeres ved
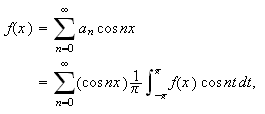
og mente dette gjaldt for alle like funksjoner. Funksjonen

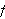 var her diskontinuerlig (trappefunksjonen vi så i kapittel 1), men
uttrykket på høyre side er jo en sum av kontinuerlige funksjoner, og
denne mente man jo var kontinuerlig. Og det var jo veldig rart, at en funksjon
som etter Eulers kontinuitetsbegrep var diskontinuerlig kunne skrives som et
uttrykk som var kontinuerlig, fortsatt etter Eulers definisjon. Fouriers
påstand i hans bok [JF, s.432] om at
var her diskontinuerlig (trappefunksjonen vi så i kapittel 1), men
uttrykket på høyre side er jo en sum av kontinuerlige funksjoner, og
denne mente man jo var kontinuerlig. Og det var jo veldig rart, at en funksjon
som etter Eulers kontinuitetsbegrep var diskontinuerlig kunne skrives som et
uttrykk som var kontinuerlig, fortsatt etter Eulers definisjon. Fouriers
påstand i hans bok [JF, s.432] om at
''Det fins ingen funksjon

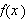 ,
eller del av funksjon, som ikke kan uttrykkes ved trigonometriske rekker'',
,
eller del av funksjon, som ikke kan uttrykkes ved trigonometriske rekker'',
må altså ses på som ''riktig'' ut fra hans begrepsapparat, men
galt etter våre dagers utvidelser. Denne feilen slet man imidlertid med
å oppdage. Til og med Cauchy ''beviste'' jo et ugyldig teorem der han
på stod en uendelig sum av kontinuerlige funksjoner selv var
kontinuerlig. Det videre arbeidet med Fourierrekker var medvirkende til at
hele analysen ble revidert, og funksjonsbegrepet var et av de temaer som fikk
en konsistent utforming. Cauchy står her sentralt. I stedet for
å basere en stringent oppbygging av analysen på algebra bygger han
den nå opp rundt en presis definisjon av limes-begrepet. I
Cours d'analyse av 1821 finner vi hans
funksjonsdefinisjon. Denne lyder [JL]:
''Når variable størrelser er knyttet sammen på en slik
måte at den ene kan bestemmes når alle de andre er kjente, betrakter
man vanligvis de forskjellige størrelsene uttrykt ved en av dem, som da
kalles den uavhengige variabel. De andre størrelsene, som uttrykkes ved
uavhengige variabel kaller vi funksjoner av denne variablen.''
Cauchy delte funksjonsbegrepet opp i enkle funksjoner og sammensatte
funksjoner. De enkle bestod av 11 funksjoner;
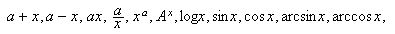
der

 og
og

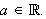 De sammensatte funksjonene kan man så lage ved å sette sammen de
enkle funksjonene på forskjellige måter. Nå begynner man
også for alvor å innse mangler ved de analytiske uttrykkene. Cauchy
viser f.eks. at
De sammensatte funksjonene kan man så lage ved å sette sammen de
enkle funksjonene på forskjellige måter. Nå begynner man
også for alvor å innse mangler ved de analytiske uttrykkene. Cauchy
viser f.eks. at

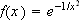 ikke kan representeres ved sin Taylorrekke i 0.
ikke kan representeres ved sin Taylorrekke i 0.
Det var også i arbeider om Fourierrekker at Eulers definisjon i praksis
ble byttet ut med sammenhengen av variabler.
Lobachevskii Note_7 og Dirichlet gjorde
dette uavhengig av hverandre (i hhv. 1834 og 1837).
Dirichlets funksjonsbegrep
I arbeidet av 1837 gir Dirichlet følgende definisjon av en funksjon [JL]:
Hvis hver

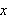 tilsvarer ett endelig
tilsvarer ett endelig

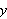 ,
slik at når
,
slik at når

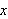 varierer fra
varierer fra

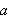 til
til

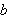 kontinuerlig, så endrer
kontinuerlig, så endrer

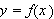 seg litt etter litt, kaller vi
seg litt etter litt, kaller vi

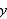 en funksjon av
en funksjon av

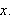
I definisjonen ser vi Dirichlet konsentrerer seg om et intervall fra

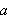 til
til

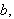 dette var nok vanskelig å fordøye for de mest konservative som
fremdeles klynget seg fast til håpet om variablens generalitet,
altså at en variabel kan anta alle verdier (helst alle komplekse verdier
og i ''verste fall'' tallinjen). Dirichlets krav om entydighet var
også noe nytt her. Dirichlet påpekte at en funksjon ikke
nødvendigvis bestemte et areal under grafen. En funksjon kunne i
følge Dirichlet være så merkelig at man ikke kunne snakke om et
areal under grafen. Som et eksempel ga Dirichlet i 1829 funksjonen
dette var nok vanskelig å fordøye for de mest konservative som
fremdeles klynget seg fast til håpet om variablens generalitet,
altså at en variabel kan anta alle verdier (helst alle komplekse verdier
og i ''verste fall'' tallinjen). Dirichlets krav om entydighet var
også noe nytt her. Dirichlet påpekte at en funksjon ikke
nødvendigvis bestemte et areal under grafen. En funksjon kunne i
følge Dirichlet være så merkelig at man ikke kunne snakke om et
areal under grafen. Som et eksempel ga Dirichlet i 1829 funksjonen
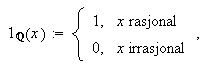
nå også kjent som Dirichlet-funksjonen
[B/N/B] og noen steder som den karakteristiske funksjonen
på 
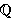 .
Dette er det første eksemplet på en funksjon som ikke er tilknyttet
et analytisk uttrykk og det skulle etterhvert dukke opp en lang rekke
funksjoner med egenskaper man ikke trodde funksjoner kunne ha.
.
Dette er det første eksemplet på en funksjon som ikke er tilknyttet
et analytisk uttrykk og det skulle etterhvert dukke opp en lang rekke
funksjoner med egenskaper man ikke trodde funksjoner kunne ha.
Hva ''er'' en funksjon i dag? En definisjon fra [TL, s. 216] / [JL, s.5]:
En funksjon

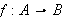 er en mengde ordnede par
er en mengde ordnede par

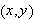 der
der

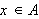 og
og

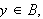 og der hver
og der hver

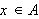 hører med til nøyaktig ett par.
hører med til nøyaktig ett par.
Integralbegrepet
Vi har vært inne på at et av problemene man møtte i forbindelse
med Fouriers løsning av varmelikningen, var meningen man skulle legge i
et uttrykk som
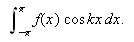
Holdningen blant vitenskapsmenn på denne tiden var at integrasjon var
antiderivasjon, hverken mer eller mindre. Etter Newtons bevis for
fundamentalteoremet hadde man gradvis gått bort fra den opprinnelige
definisjonen av integralet som grensen for en sum, og i stedet konsentrert seg
om antiderivasjon. Kanskje var begeistringen over og nytten av det fantastiske
fundamentalteoremet så stor at man glemte den opprinnelige ideen? Det
ubestemte integralet
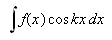
''var'' i 1807 altså en funksjon som hadde

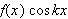 som derivert. Og dette ble et problem. Det er selvsagt ikke tilfelle at man
alltid kan finne et eksplisitt uttrykk hvor den deriverte av denne blir det vi
ø nsker, f.eks.
som derivert. Og dette ble et problem. Det er selvsagt ikke tilfelle at man
alltid kan finne et eksplisitt uttrykk hvor den deriverte av denne blir det vi
ø nsker, f.eks.

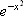 .
Med Fouriers beregninger fikk man igjen bruk for at integralet var arealet
under en kurve. Noe som førte til et nytt problem; hva
er et areal? (De var selvfølgelig klare over at arealer under
.
Med Fouriers beregninger fikk man igjen bruk for at integralet var arealet
under en kurve. Noe som førte til et nytt problem; hva
er et areal? (De var selvfølgelig klare over at arealer under

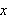 -aksen
måtte tolkes som negative bidrag). Man kunne vel tenke seg
å definere areal som integralet av en eller annen funksjon, men da
går man i ring. Vi må altså finne en annen definisjon av
integralet.
-aksen
måtte tolkes som negative bidrag). Man kunne vel tenke seg
å definere areal som integralet av en eller annen funksjon, men da
går man i ring. Vi må altså finne en annen definisjon av
integralet.
En annen morsom detalj er at det var Fourier som var først til
å sette grenser på integraltegnet, som f.eks.

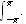 Tidligere hadde grensene blitt angitt kun med ord. Faktisk var det
også Fourier som introduserte tegnet
Tidligere hadde grensene blitt angitt kun med ord. Faktisk var det
også Fourier som introduserte tegnet

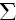 som summasjonssymbol [JP, s.7].
som summasjonssymbol [JP, s.7].
I Dirichlets bevis for konvergens av Fourierrekker krevde han at

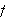 må tte være integrerbar over
må tte være integrerbar over

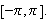 Det at en funksjon er integrerbar forandret også betydning etter hvert. I
flere omganger fulgte nye definisjoner av integralbegrepet. Cauchy i
1820-å rene, Riemann Note_8 i
1860-årene, Darboux Note_9 i 1875
og Lebesgue i 1902 ga alle slike definisjoner. Vi skal fort gå gjennom
hovedtrekkene i de forskjellige epokene.
Det at en funksjon er integrerbar forandret også betydning etter hvert. I
flere omganger fulgte nye definisjoner av integralbegrepet. Cauchy i
1820-å rene, Riemann Note_8 i
1860-årene, Darboux Note_9 i 1875
og Lebesgue i 1902 ga alle slike definisjoner. Vi skal fort gå gjennom
hovedtrekkene i de forskjellige epokene.
Cauchy-integralet
Cauchy var den første som definerte integralet som en grense for en sum
[TL1, s. 380].
Kva med Newton og Leibniz!comment
Ved noen revolusjonerende forelesninger ved Ecole Polytechnique i 1820-å
rene la han frem sin definisjon. Integralet ble definert slik:
Figuren under illustrerer Cauchys ide om at vi ikke har noen valgmuligheter
når partisjonen er gitt. Funksjonen passerer gjennom øvre venstre
hjø rne av hver søyle med bredde

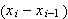 og høyde
og høyde

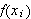 :
:
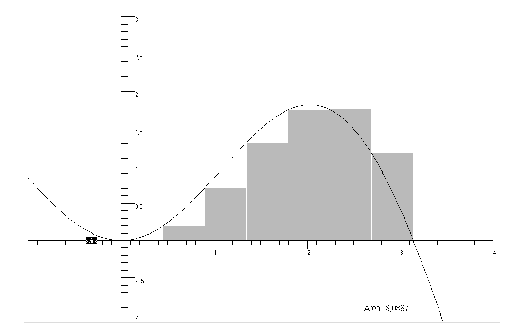
Cauchy-integralet
Vi skal i neste kapittel se hvordan Dirichlet beviste konvergens av
Fourierrekker, og det var da Cauchys integralbegrep man hadde for hånden.
Riemann-integralet
Riemann-integralet er et noe mer fleksibelt verktøy enn Cauchys integral.
Kanskje er dette også det mest kjente integralbegrepet. Han var nok
inspirert av Cauchy, men i stedet for å være bundet til et punkt i
venstresiden av partisjonsintervallet tillater Riemann at funksjonen vi skal
integrere skjærer toppen av søylene på partisjonsintervallene i
et vilkårlig punkt i intervallet. Heldigivis er disse to
integralbegrepene ekvivalente. Det er tross alt snakk om det samme arealet. En
funksjon er integrerbar etter Cauchys definisjon av integralet hvis og bare
hvis den er integrerbar etter Riemanns integraldefinisjon, og verdien av
integralet er den samme, men det er ikke trivielt å bevise det.
Figuren under illustrerer Riemanns ide.
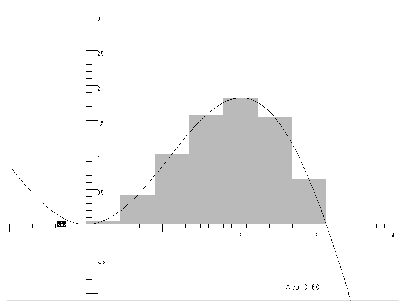
Riemann-integralet
Merk at Riemann ikke nødvendigvis holdt seg til
midtpunktet av intervallet, slik som på figuren, men kunne velge

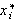 fritt inne i det aktuelle intervallet. Vi skal se på enda en variant av
integralbegrepet.
fritt inne i det aktuelle intervallet. Vi skal se på enda en variant av
integralbegrepet.
Darboux-integralet
Etter Riemanns definisjon av integralet, skulle også Darboux komme med et
integralbegrep (1875). Denne definisjonen var kanskje enda litt mer elegant
enn Riemanns versjon. Det kan vises at vi ikke får noen utvidelser av det
integralbegrepet vi har definert foran, men en annen måte å definere
integralet på (Selv om Darboux-integralet er det som introduseres i mange
lærebøker kommer det kanskje ikke alltid fram at det er Darboux'
definisjon vi snakker om)! Vi finner i [TL1, s.322ff] en gjennomgang av
Darboux-integralet. Det vi trenger i Darboux' definisjon er at funksjonen er
begrenset. Det gir da mening å snakke om

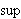 og
og

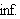
Vi lar igjen

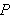 være en partisjon
være en partisjon
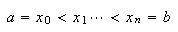
av

![$\left[ a,b\right] $](begrep__102.png) der intervallene mellom partisjonspunktene ikke nø dvendigvis er like
lange. Idéen til Darboux var å tilnærme funksjonen
der intervallene mellom partisjonspunktene ikke nø dvendigvis er like
lange. Idéen til Darboux var å tilnærme funksjonen

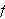 vi ønsker å integrere med rektangler
både under og over funksjonen. Ved å sette
vi ønsker å integrere med rektangler
både under og over funksjonen. Ved å sette
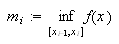
og
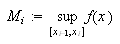
får vi følgende formler for øvre sum

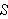 og nedre sum
og nedre sum

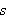 (også kalt oversum og undersum) for arealet under grafen,
(også kalt oversum og undersum) for arealet under grafen,
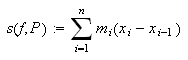
og
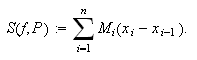
Tilsvarende defineres øvreintegralet
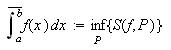
og
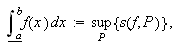
der

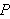 gjennomløper alle partisjoner av
gjennomløper alle partisjoner av

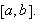 Vi kan da gi følgende definisjon:
Vi kan da gi følgende definisjon:
Ser vi på eksemplet med Dirichletfunksjonen i () ser vi at denne fortsatt
ikke er integrerbar. Uansett hvordan vi velger vå re partisjonspunkter
vil alle intervall inneholde rasjonale og irrasjonale tall. Siden
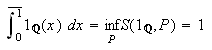
og

uansett hvilke partisjoner

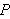 vi ser på, så er ikke
vi ser på, så er ikke

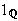 integrerbar.
integrerbar.
Også denne integraldefinisjonen er ekvivalent med Riemann og Cauchys
definisjoner, men det er imidlertid ikke helt trivielt å vise dette (se
for eksempel [TL1, s.348]).
Lebesgue-integralet
Selv om Riemann-integralet kanskje er det mest kjente, er likevel
Lebesgue-integralet det mest brukte i avansert
litteratur. Se for eksempel [R, s.77ff]. Lebesgue snudde på en måte
Riemann-integralet på siden. I stedet for å dele arealet under en
graf opp i søyler, delte han det opp i horisontale nivåer, som
automatisk partisjonerer definisjonsområdet. Legg igjen merke til hvor
enkel ideen er! Et eksempel fra [B/B/T, s.60f]: Tenk at du trekker mynter opp
av lommen og skal telle hvor mye penger du har. Du kan gjøre det
på to måter:
-
Tell pengene i den rekkefølge du plukker dem opp, f.eks. 10kr + 5kr + 1kr
+ 1kr + 5kr = 22kr.
-
Gruppér pengene etter verdi, altså 1 tier + 2 femmere + 2
kronestykker = 22kr
Første regnemåte tilsvarer Riemanns integralmetode, mens andre
måte tilsvarer Lebesgue-integralet. Lebesgues integral bygger
på målteori. Veldig kort fortalt: et
mål er en funksjon

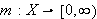 ,
der
,
der

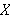 er en klasse av delmengder av
er en klasse av delmengder av

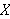 .
Denne funksjonen tilordner et reelt tall til en mengde i
.
Denne funksjonen tilordner et reelt tall til en mengde i

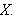 Dette kan ses på som en slags størrelsesmål på mengden.
Ser vi igjen på eksemplet med pengene kan vi si at målene
på pengene er myntverdien, 1, 5 eller 10. Ved Lebesgue-integrasjon
summerte vi altså hvor mange mynter vi hadde av hver bestemt verdi. Dette
konseptet overfører vi nå til funksjoner.
Dette kan ses på som en slags størrelsesmål på mengden.
Ser vi igjen på eksemplet med pengene kan vi si at målene
på pengene er myntverdien, 1, 5 eller 10. Ved Lebesgue-integrasjon
summerte vi altså hvor mange mynter vi hadde av hver bestemt verdi. Dette
konseptet overfører vi nå til funksjoner.
Et viktig poeng ved Lebesgue-teorien er at vi kan tillate oss å se bort
fra integralet over mengder med mål 0, som for eksempel de rasjonale
tallene
 Først deles den vertikale aksen opp med en partisjon
Først deles den vertikale aksen opp med en partisjon
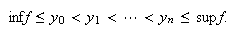
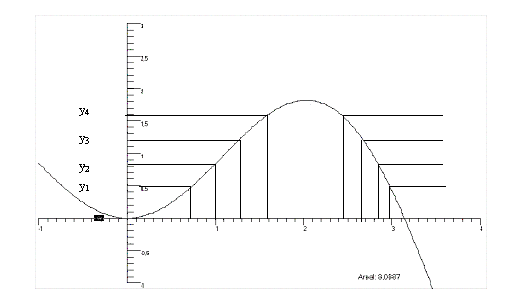
Lebesgue-integralet
Dernest lar vi

 På figuren blir da
På figuren blir da

 unionen av to halvåpne intervaller. Vi har da fått en partisjon
unionen av to halvåpne intervaller. Vi har da fått en partisjon
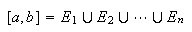
der

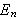 er parvis disjunkte. Vi danner summene
er parvis disjunkte. Vi danner summene
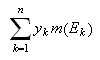
og
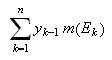
som en tilnærming av arealet under grafen. Vi må da forlange at det
inverse bildet av

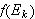 tilhører de mengdene som vi kan anvende mål-funksjonen på. Vi
snakker da om at
tilhører de mengdene som vi kan anvende mål-funksjonen på. Vi
snakker da om at

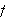 er målbar. Hvis
er målbar. Hvis

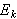 -mengdene
er forholdsvis enkle, som for eksempel en endelig union av intervaller,
så vil situasjonen være omtrent som i Riemann-integralet. Men
-mengdene
er forholdsvis enkle, som for eksempel en endelig union av intervaller,
så vil situasjonen være omtrent som i Riemann-integralet. Men

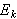 kan være mer kompliserte, for eksempel trenger de ikke å inneholde
noe intervall i det hele tatt, jf. Dirichlet-funksjonen. Vi trenger en grundig
gjennomgang av begrepene målbare funksjoner og målbare mengder
skulle vi fulgt Lebesgue--teorien til bunns. Hvis vi kan få disse to
summene vilkårlig nær hverandre sier vi at
kan være mer kompliserte, for eksempel trenger de ikke å inneholde
noe intervall i det hele tatt, jf. Dirichlet-funksjonen. Vi trenger en grundig
gjennomgang av begrepene målbare funksjoner og målbare mengder
skulle vi fulgt Lebesgue--teorien til bunns. Hvis vi kan få disse to
summene vilkårlig nær hverandre sier vi at

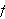 er Lebesgue-integrerbar og integralet
er Lebesgue-integrerbar og integralet

 er den felles grensen for
summene
er den felles grensen for
summene
 Med en slik definisjon av integralet kan vi igjen ta for oss Dirichlets
funksjon i (). Vi ser bort fra de mengdene som har mål 0, det vil si de
rasjonale tallene. Verdien av integralet blir da
Med en slik definisjon av integralet kan vi igjen ta for oss Dirichlets
funksjon i (). Vi ser bort fra de mengdene som har mål 0, det vil si de
rasjonale tallene. Verdien av integralet blir da
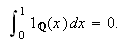
Lebesgue viste også at det fins ikke-målbare funksjoner. Disse kan
da ikke integreres, ut fra hans definisjon av integralet. Det kan faktisk
vises at det ikke lar seg gjøre å lage et integralbegrep som er slik
at vi kan integrere alle funksjoner med det funksjonsbegrep vi
nå benytter [TL1].
Konvergens
Også her har man sett eksempler på voldsomt engasjement.
Abel Note_10 skrev som kjent;
''Divergente rækker er i det hele noget fandenskab, og det er en skam at
man vover at begrunde nogen demonstration derpå.''
De viktigste spørsmålene om Fourierrekker er (og var
også på Fouriers tid) når de
konvergerer. Problemer dukket da naturlig nok opp, da man ikke hadde noe
veletablert konvergensbegrep. I våre dager benytter vi flere typer
konvergens. Fourierrekker kan således også konvergere
på forskjellige måter. Eksempler på dette er konvergens i

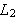 -norm
og i Cesaro-middel (se f.eks. [B/N/B]). De to vanligste formene for konvergens
er imidlertid punktvis og uniform konvergens.
-norm
og i Cesaro-middel (se f.eks. [B/N/B]). De to vanligste formene for konvergens
er imidlertid punktvis og uniform konvergens.
Dette er en naturlig definisjon av konvergens og var nok også denne man
hadde i tankene på Fouriers tid. Det høres fornuftig ut å si at
en funksjon konvergerer mot en grense dersom den konvergerer for hver

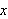 .
En stor ulempe ved punktvis konvergens er det likevel. Man kan ikke integrere
en punktvis konvergent rekke ledd for ledd og være sikret
å få samme integralverdi som ved å integrere grensefunksjonen.
Vi husker at Fourier benyttet seg av
.
En stor ulempe ved punktvis konvergens er det likevel. Man kan ikke integrere
en punktvis konvergent rekke ledd for ledd og være sikret
å få samme integralverdi som ved å integrere grensefunksjonen.
Vi husker at Fourier benyttet seg av
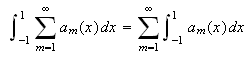
for å finne formelen for Fourierkoeffisientene. Siden en uendelig sum er
grensen for følgen av partialsummer må vi betrakte problemet som
ombytte av integrasjon og grensebetraktning. Vi setter ovenfor

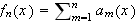 og ser på følgen
og ser på følgen

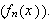 Betrakt følgende klassiske eksempel, som viser at
Betrakt følgende klassiske eksempel, som viser at
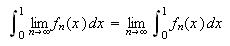
ikke holder generellt:
Man kan altså generelt ikke gjøre som Fourier. Vi synes kanskje ikke
dette er så rart, med alle skrekkeksempler på hva som skjer ved
uendelige prosesser. Vi trenger strengere krav til en funksjonsfølge skal
vi kunne integrere den ledd for ledd. Cauchy introduserte remediet i 1826;
uniform konvergens.
Dette er en sterk antakelse, men vi kan da vise at leddvis
integrasjon holder [PRA, s.54].
I forbindelse med Fourierteori ser vi også klart forskjellen
på uniform og punktvis konvergens av rekker. Denne forskjellen
illustreres med Gibbs fenomen i et tillegg.
Litteratur


This document created by Scientific WorkPlace 4.0.
Neste: Fourierrekker
Forrige: Varmelikningen

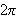 -periodisk
og kontinuerlig, og som hadde Fourierrekke som divergerte i et punkt [TWK,
s.67]. Men Fourier påsto jo at alle funksjoner
kunne representeres ved Fourierrekker som konvergerer mot funksjonen! Hvordan
skulle man da kunne ha en ''pen'' Fourierteori? Nå må vi tenke oss
til holdningen Fouriers samtid hadde til matematikk. Man skulle ha en
helhetlig vitenskap, og analysen skulle være generelt gyldig innenfor en
passende valgt klasse av funksjoner. Med slike funksjoner som Du Bois-Reymond
la fram, så det ut til at man måtte skreddersy funksjonsklasser
avhengig av hvilket problem man studerte. Dette var en
vanskelig tanke for to hundre år siden, og ble nok oppfattet som
matematisk fusk. Vi kan kanskje se for oss flere veier ut av uføret:
-periodisk
og kontinuerlig, og som hadde Fourierrekke som divergerte i et punkt [TWK,
s.67]. Men Fourier påsto jo at alle funksjoner
kunne representeres ved Fourierrekker som konvergerer mot funksjonen! Hvordan
skulle man da kunne ha en ''pen'' Fourierteori? Nå må vi tenke oss
til holdningen Fouriers samtid hadde til matematikk. Man skulle ha en
helhetlig vitenskap, og analysen skulle være generelt gyldig innenfor en
passende valgt klasse av funksjoner. Med slike funksjoner som Du Bois-Reymond
la fram, så det ut til at man måtte skreddersy funksjonsklasser
avhengig av hvilket problem man studerte. Dette var en
vanskelig tanke for to hundre år siden, og ble nok oppfattet som
matematisk fusk. Vi kan kanskje se for oss flere veier ut av uføret:
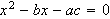
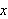
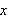
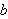
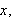
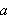
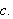
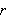
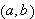
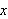
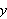
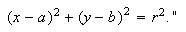
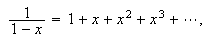
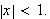
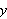
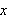
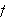
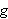
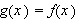
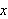
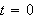

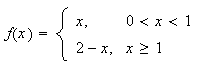
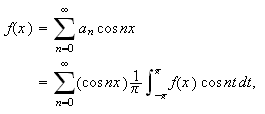
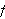
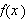
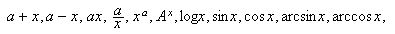
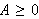
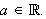
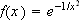
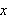
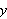
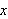
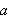
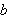
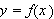
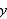
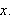
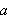
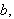
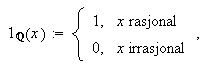
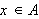
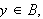
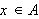
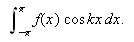
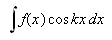
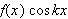
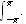
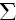
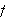
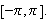
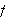
![$\left[ a,b\right] $](begrep__73.png)
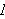
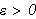
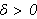
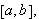

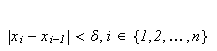
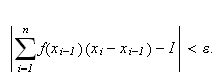

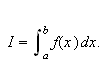
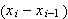
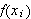

![$\left[ a,b\right] $](begrep__86.png)
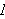
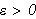
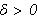
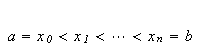
![$\left[ a,b\right] $](begrep__91.png)
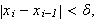
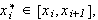
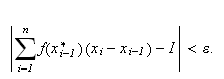
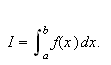

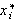
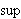
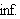
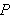
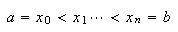
![$\left[ a,b\right] $](begrep__102.png)
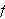
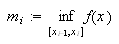
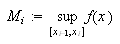
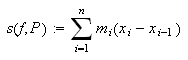
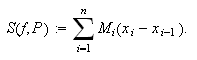
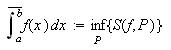
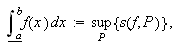
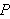
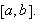
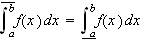
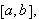
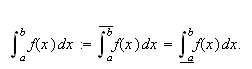
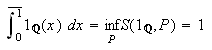

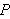
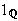
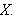

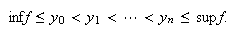

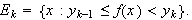
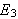
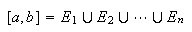
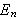
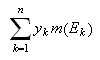
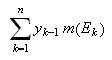
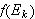
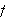
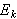
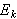
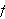


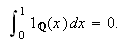
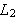
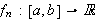

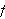
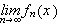
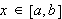
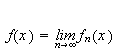
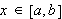
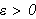
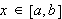
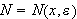
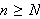

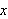
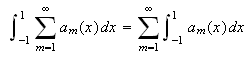
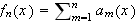
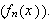
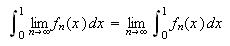
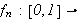
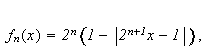

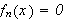
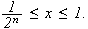
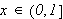
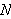
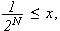
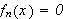
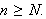
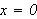
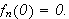
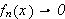
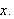
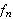
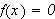

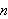
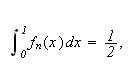
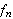
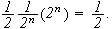


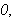
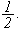
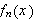
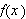
![$\left[ a,b\right] $](begrep__189.png)