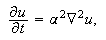
der
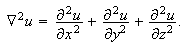
Denne kalles Laplaceoperatoren. La oss først stille opp divergensteoremet for referansens skyld:
Vi har (kap. 2) utledet varmelikningen ut fra fysiske betraktninger i en
dimensjon. En annen måte er å benytte Gauss'
divergensteorem. Dette er skissert i [E/P, s.956], og det skal vi se
litt på nå. Varmelikningen i tre dimensjoner
er
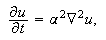
der
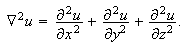
Denne kalles Laplaceoperatoren. La oss først
stille opp divergensteoremet for referansens skyld:
[E/P] Anta

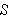 er en lukket, stykkevis glatt flate som avgrenser det romlige området
er en lukket, stykkevis glatt flate som avgrenser det romlige området

 La
La

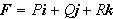 være et vektorfelt der komponentfunksjonene
være et vektorfelt der komponentfunksjonene

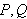 og
og

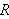 har kontinuerlige fø rste ordens partielle deriverte
på
har kontinuerlige fø rste ordens partielle deriverte
på 
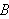 .
La
.
La

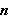 være den ytre normale enhetsvektoren til
være den ytre normale enhetsvektoren til

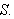 Da er
Da er
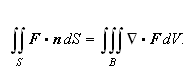
der
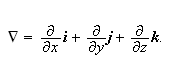
Vi skal nå se på hvordan vi, på en litt mer moderne måte
enn Fourier, kan komme fram til at en temperatur

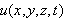 i punktet
i punktet

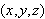 ved tiden
ved tiden

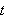 måtte tilfredsstille likningen
måtte tilfredsstille likningen
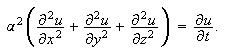
Anta vi har et vilkårlig legeme

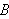 med flate
med flate

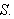 Som før lar vi
Som før lar vi

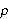 være tettheten,
være tettheten,

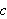 spesifikk varmekapasitet og
spesifikk varmekapasitet og

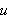

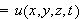 temperaturen ved tiden
temperaturen ved tiden

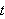 i posisjonen
i posisjonen

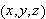 i legemet. Temperaturen antas å være glatt. Volumelementet
i legemet. Temperaturen antas å være glatt. Volumelementet

 har massen
har massen

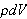 .
Varmemengden som trengs for å varme 1
cm
.
Varmemengden som trengs for å varme 1
cm
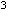 1 grad er
1 grad er

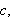 så
så 
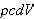 er det som må tilføres for å varme volumelementet 1 grad.
Varmemengden som må tilføres
er det som må tilføres for å varme volumelementet 1 grad.
Varmemengden som må tilføres

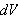 for å varme dette
for å varme dette

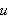 grader er da
grader er da

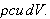 Varmemengden (eng.: heat content)
Varmemengden (eng.: heat content)

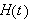 i legemet
i legemet

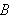 ved tiden
ved tiden

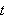 er derfor
er derfor
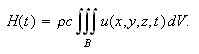
Vi antar derivasjon under integraltegnet er tillatt, og raten varmemengden i

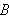 endres med pr. tidsenhet ved tiden
endres med pr. tidsenhet ved tiden

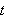 er
er
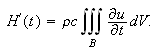
Den eneste måten varmemengden inne i

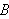 kan forandres på (når vi ser bort fra at den øker eller avtar
på grunn av kjemiske reaksjoner) er at varmeendringen skjer på grunn
av strømning gjennom flaten
kan forandres på (når vi ser bort fra at den øker eller avtar
på grunn av kjemiske reaksjoner) er at varmeendringen skjer på grunn
av strømning gjennom flaten

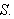 I det endimensjonale tilfelle er varmestrømmen proporsjonal med
størrelsen til gradienten og flyter i negativ retning. Hvis vi da ser
på et flateelement
I det endimensjonale tilfelle er varmestrømmen proporsjonal med
størrelsen til gradienten og flyter i negativ retning. Hvis vi da ser
på et flateelement

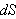 med normalvektor
med normalvektor

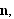 så er
så er

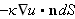 strømmen av varme inn eller ut gjennom denne flaten, der
strømmen av varme inn eller ut gjennom denne flaten, der

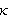 er termisk konduktivitet. Total varmemengde pr. tidsenhet ved tiden
er termisk konduktivitet. Total varmemengde pr. tidsenhet ved tiden

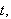 som når fram til
som når fram til

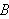 gjennom flaten
gjennom flaten

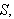 er da
er da
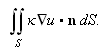
Uttrykket i () må være lik det i (), altså
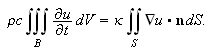
Divergensteoremet gir at
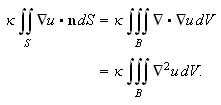
Det vil si
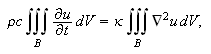
som gir
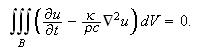
Volumet

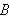 var tilfeldig valgt og temperaturen
var tilfeldig valgt og temperaturen

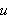 er antatt å være glatt. Skal integralet være 0 på alle
slike områder
er antatt å være glatt. Skal integralet være 0 på alle
slike områder

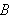 må da integranden være eksakt lik
må da integranden være eksakt lik

 .
Altså
.
Altså
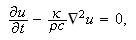
eller
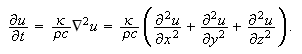
| \lbrack E/P] | Edwards, C.H../Penney, D.E.: Calculus with analytic geometry |
| Prentice Hall Inc. (1994); ISBN: 0-13-176728-3 |
Neste: Fubinis teorem