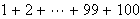ved å sette opp 
?Johann Friedrich Carl Gauss (1777-1855), stor, tysk matematiker som også var veldig aktiv i andre vitenskaper. Vi har blant annet Gausskurve i sannsynlighetsteorien eller Gaussflate i el-lære. Kanskje har noen hørt om niårige Gauss som regnet ut 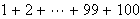ved å sette opp ?
Marie Ennemond Camille Jordan (1838-1922), fransk matematiker (hankjønn til tross for navnet) som arbeidet mest innen geometri og symmetrigrupper. Vi har mange begrep fra Jordan, eksempel på det er Jordan-kurve, Jordan-kanonisk form og Gauss-Jordan eliminasjon.
Leopold Fejér (1880-1959), ungarsk matematiker som i hovedsak studerte Fourierrekker og deres singulariteter. Fejér ble noen få år før han kom med sine resultater sett på som så svak i matematikk at han måtte ha spesialundervisning.
James Mercer (1883-1932), britisk matematiker som gjorde seg bemerket innen integral-likninger og rekkeutvidelser med ortogonal basis.
Pierre Bonnet (1819-1892), fransk matematiker som arbeidet mest med differensial- geometri. Publiserte også arbeider innen kartografi, algebra, mekanikk og matematisk fysikk.
Se definisjon av Cauchy-integralet i forrige kapittel. Cauchy-integralet er ikke regnet som like anvendbart som Riemann-integralet, men kanskje dette er et av de stedene det kommer mest til sin rett?