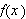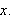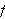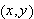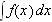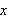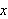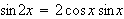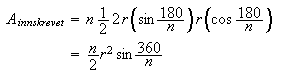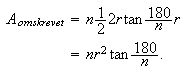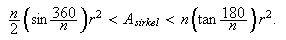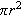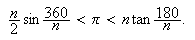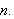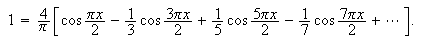PARALLELL TIL UNDERVISNING
I Læreplanen finner vi følgende:
''Matematikk har lange historiske tradisjoner og har alltid vært en
viktig del av vår kultur. (...) Opplæringen i faget har som mål
at elevene utvikler innsikt i matematikkens historie og fagets rolle i kultur
og vitenskap.''
Dette utdraget fra læreplanen viser at matematikkens historie står
sterkere i skolematematikken enn på lenge. Vi aner kanskje en sammenheng
mellom Fouriers problemer og det elever og studenter sliter med, både i
den videregående skolen og på høgere nivå. Vi skal
nå se en gang til på disse begrepene i dagens skole.
Et par pedagogiske begrep som står sentralt i den forbindelse:
-
Assimilering - Det vil se hvordan man setter gammel
kunnskap i sammenhenge med ny kunnskap. Altså hvordan man binder sammen
det man vet fra før, med det man skal lære.
-
Skjematenkning - Begrepet skjema betegner det mentale
bildet hver enkelt danner seg av et bestemt lærestoff.
I boken Thinking mathematically [JM], som er brukt i
læ rerutdanningen, trekkes det opp strategier for hvordan matematiske
problemer kan løses. Flere begreper som blir drøftet i denne boken
passer godt inn i forløpet til problemet med konvergens av Fourierrekker:
-
Getting involved , er et sentralt aspekt ved
å tenke matematisk. Fourier selv var jo i høyeste grad veldig
involvert på den måten at det var nøye undersøkelser og
eksperimenter med varme som gjorde at han utviklet nye matematiske ideer.
-
Et annet begrep er mulling (vi har noe av det samme
på norsk, når vi sier at tankene kverner rundt), som symboliserer at
man ikke helt lar et problem slippe unna tankene, selv om man ikke har fokus
100% på det hele tiden.
-
Til slutt oppnår man forhåpentligvis insight
, noe man også godt kunne kalt ''A-ha-opplevelsen''. En slik kunne for
eksempel være å oppdage sammenhengen mellom Fourier-koeffisienter
integraler.
-
Kanskje det beste eksemplet på at Fourierteorien følger
mønsteret i løsningen av et standardproblem er begrepet
stuck. Som det blir sagt i [JM]: ''Being STUCK is a
great state!''. Hva menes med dette? Jo, forfatteren mener at det
å være stuck er en veldig viktig del av den
kreative prosessen. Poenget er at det er da man virkelig har muligheten til
å lære noe nytt! Slik er det nok også med elever og studenter i
dag. Når de står virkelig fast, har de en gylden mulighet til
å tilegne seg dypere forståelse av problemet. Kanskje ligger det noe
å ta fatt i her; i undervisningsprosesser i dag er det ofte en sovepute
for elevene at man får løsninger ferdige servert
før man har stått fast selv. Poenget
må jo være at man ved være stuck vet
hva vanskelighetene stikker i, og dermed får bedre utbytte av
å få en løsning på problemet, eventuelt gitt av andre.
Har vi i dag noe hjelpemiddel for å hjelpe elever og studenter gjennom
disse fasene? Et virkemiddel som Fouriers samtid iallfall ikke var i
besittelse av var datamaskiner. Datamaskiner i undervisningen er ofte uglesett
av mange. En kritikk man med rette kan anvende, er at man ikke er i stand til
å bevise noenting ved hjelp av en datamaskin. Men
som en pekepinn på vei til et resultat kan de være til uvurderlig
hjelp.
I tillegg C finner vi en beskrivelse av Gibbs fenomen. Dette fenomenet ble jo
oppdaget nettopp på grunn av at
Michelson Note_1 hadde matet en maskin
(sannsynligvis en primitiv form for regnemaskin) med en datamengde han mente
var tilstrekkelig for å få resultatet han ønsket. Men når
han senere studerte partialsummene i Fourierrekka han undersøkte, ble han
ikke kvitt de ''hattene'' som vi nå altså kjenner som Gibbs fenomen
- og som vi vet skyldes forskjellen mellom punktvis konvergens og uniform
konvergens.
Funksjonsbegrepet
Elever i videregående skole kommer gjerne til høyere utdanning med
forestillingen om at en funksjon er en kurve i planet (eller som mange elever
tror; en strek på papiret), og framstillingen man etterhvert kommer til,
nemlig at det dreide seg om sammenhenger mellom variable, kunne vært
klarere presist. Studenter i NTNU-faget MNFMA001 (for mange det fø rste
møte med flerdimensjonal analyse) møter for eksempel funksjoner som
beskriver temperatur i rommet, kanskje er de av typen

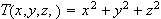 .
Hvordan skal man kunne assimilere et slikt begrep hvis man er fastlåst
til sine gamle begreper, og samtidig skulle tro man er i stand til
å tegne en slik funksjon? Og hvem fikk vel høre i 2MX / 3MX at det
fins funksjoner av typen
.
Hvordan skal man kunne assimilere et slikt begrep hvis man er fastlåst
til sine gamle begreper, og samtidig skulle tro man er i stand til
å tegne en slik funksjon? Og hvem fikk vel høre i 2MX / 3MX at det
fins funksjoner av typen

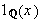 som nevnt tidligere? Man kan vel innvende at slike funksjoner ikke bør
stå sæ rlig sentralt i videregående skoles matematikk-pensum,
men det må vel ligge et poeng i å vite at de fins? I alle fall burde
lærerne være klar over situasjonen.
som nevnt tidligere? Man kan vel innvende at slike funksjoner ikke bør
stå sæ rlig sentralt i videregående skoles matematikk-pensum,
men det må vel ligge et poeng i å vite at de fins? I alle fall burde
lærerne være klar over situasjonen.
En måte å illustrere en slik sammenheng på, og som kan
forstås tidlig, er ved den gode, gamle ''funksjonsmaskinen''. (Finnes
faktisk i Tambs-Lyches analysebøker). For å vise at man ikke er
fastlåst til et enkelt uttrykk, kan man demonstrere med en maskin som
produserer

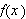 etter hvert som den blir matet med
etter hvert som den blir matet med

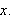 Og at
Og at

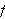 bare er navnet på maskinen. En slik Petter Smart-maskin viser på en
fin måte at det dreier seg om samhørende verdier
bare er navnet på maskinen. En slik Petter Smart-maskin viser på en
fin måte at det dreier seg om samhørende verdier

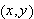 og at man ikke nødvendigvis har formler som beskriver enhver funksjon i
matematikken. Assimilering av funksjonsbegrepet kunne da kanskje skjedd
på en annen måte enn hvis man gyver rett løs på bruk av
grafiske framstillinger. Dette kan jo også lett demonstreres med en
datamaskin. Visse websider tar også for seg et slikt skjema ved
å lage en interaktiv maskin der elever kan putte hva som helst oppi og
observere hva som kommer ut.
og at man ikke nødvendigvis har formler som beskriver enhver funksjon i
matematikken. Assimilering av funksjonsbegrepet kunne da kanskje skjedd
på en annen måte enn hvis man gyver rett løs på bruk av
grafiske framstillinger. Dette kan jo også lett demonstreres med en
datamaskin. Visse websider tar også for seg et slikt skjema ved
å lage en interaktiv maskin der elever kan putte hva som helst oppi og
observere hva som kommer ut.
Et slikt skjema, er også fruktbart med tanke på senere anvendelser i
programmering av datamaskiner. Da skal man gjerne finne et uttrykk som
tilsynelatende ikke har med grafer å gjøre, men snarere sammenhenger
mellom input og output.
Integralbegrepet
Ved høgere utdanning ergrer man seg ofte over nye studenters oppfatning
av integralbegrepet. Tendensen har i lang tid vært at elever i
videregående skoler sitter med oppfatningen at integrasjon er
nøyaktig det samme som antiderivasjon. Selv om hverken lærere eller
skolebøker legger fram akkurat denne påstanden, så burde
kanskje situasjonen blitt klarere framstilt for elevene. At en slik oppfatning
er uheldig også med tanke på videre studium er opplagt (og
velkjent). En elev som lærer å regne ut de integralene han/hun blir
presentert for i videregående skoles matematikk kan nok miste noe av
motivasjonen når en på universitet og høgskoler begynner
å lage Riemann-summer. Lang tid brukes for
å få fundamentalteoremet etablert. ''Hva er vitsen med
å gjøre det så tungvint?'' (Hva slags skole har man havnet
på hvis man ikke vet at det er bare å antiderivere?) Ergrelsen er
vel heller ikke så vanskelig å forstå. På en måte kan
man si at mange elever har det samme problemet matematikerne hadde
på Fouriers tid med at man hadde sett seg blind
på fundamentalteoremet. Og hva er det egentlig som er hovedtanken i
skolen? Hva er viktigst; skal elevene forstå begrepene og teorien bak,
eller skal de være i stand til å bruke ferdige formler til
å komme med håndfaste resultater?
Grensebegrepet er nok vanskelig, men ville det ikke være mer næ
rliggende for skoleelever å tenke seg integralet som grensen for sum av
tynne biter enn som en antiderivert?
Et eksempel fra virkeligheten: En skoleklasse (3MX) på 11 elever fikk
spørsmålet ''hva er et integral?'' Ti av elevene svarte
''antiderivasjon''.
Kanskje er også skolebøkene for uklare på dette området.
Det trengs kanskje ikke så mye for å pensle elevene inn på rett
spor heller. Se på de første linjene i en eldre utgave av boken
2MN [S/Ø].
''I dette kapitlet skal vi lære å integrere funksjoner. Det skriver
vi slik:

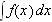 .
Vi kan tolke integrasjonen geometrisk som å finne arealet mellom grafen
til en funksjon og
.
Vi kan tolke integrasjonen geometrisk som å finne arealet mellom grafen
til en funksjon og

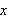 -aksen.''
-aksen.''
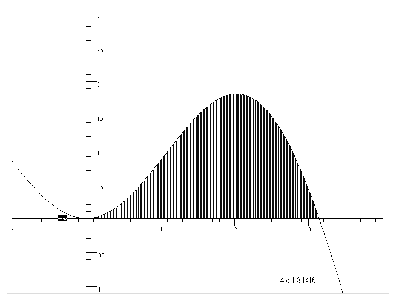
Figur for å illustrere
Leibniz' ''uendelige sum av uendelig tynne rektangler''
Leser man litt videre i denne introduksjonen kommer man straks
innpå Leibniz' tanker om at integrasjon var å summere ''alle tynne
linjer'' under en graf. Da kan vel ikke veien være særlig lang til
å skjø nne hovedideen? Riktignok nevnes ikke at integralet av en
funksjon som ligger under

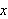 -aksen
kommer ut som negativt og dermed vanskelig kan ses på som et areal, men
dette kommer man inn på litt senere.
-aksen
kommer ut som negativt og dermed vanskelig kan ses på som et areal, men
dette kommer man inn på litt senere.
En måte å takle dette problemet på i undervisningen er for
eksempel å ta i bruk IKT-hjelpemidler. Programvare til bruk i
undervisningen er gjerne uglesett både av lærere og pedagoger, men
akkurat i tilfellet innføring av integrasjonsbegrepet kan de etter min
mening så absolutt finne sin plass. Et kjent pedagogisk prinsipp er at
elever må presenteres for mange eksempler innenfor en kort tidsperiode
for å lære et nytt begrep. Riemann-summer tar imidlertid ganske lang
tid å illustrere om man skal tegne og regne på et stort antall
søyler for hånd. Etter å ha prøvd det ett par ganger for
hånd kan man gjerne overlate til et dataprogram å ytterligere
få klarhet i begrepet. Med IKT kan man på kort tid presentere mange
situasjoner som illustrerer konseptet med arealet under en graf som grensen
for en sum.
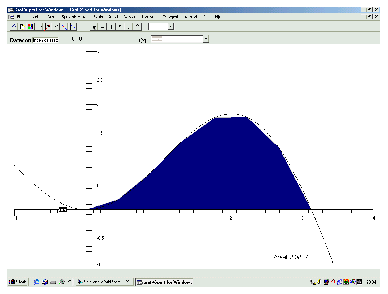
Illustrasjon av
trapes-metoden.
Selve eksperimentet blir det samme med slikt verktøy, men med slike
hjelpemiddel kan elever selv forandre antallet søyler til praktisk talt
så mange de vil. Man trenger ikke tenke på de regnetekniske
vanskelighetene i første omgang, men bare studere selve egenskapen til
integralbegrepet. Funksjonen kan selvfølgelig raskt endres,
integrasjonsmetoden likeså (Simpsons metode, trapesmetoden, osv).
Nå når matematikkens historie stadig blir mer vektlagt i skolen
(L97) kan man kanskje se langt bak i tiden for å få noen gode ideer
med tanke på innføring av integralet. Hvordan startet det hele? Det
er nesten ikke grenser for hvor langt tilbake man kan spore selv
integrasjonsideen. Ideen er jo enkel; ''mange bekker små blir en stor
å''. Allerede Arkimedes Note_2 hadde
en slags integralteknikk. Et kjent eksempel er måten han fant arealet av
en sirkel på. La oss se på hvordan han kunne finne et slikt areal
ved å anvende en tenkemåte lik den vi prøver
å overføre til elevene [TL2]. Arkimedes ville regne ut arealet av en
sirkelen og ideen hans var å tilnærme dette arealet med arealer han
behersket utregningen av. Han laget en omskreven og en innskreven mangekant i
sirkelen, og denne delte da opp sirkelen i innskrevne og omskrevne trekanter
(For øvrig kan alle mangekanter deles opp i
trekanter - et viktig poeng i ungdomsskolen!). Jf., Darboux's ideer. Se
figuren under.
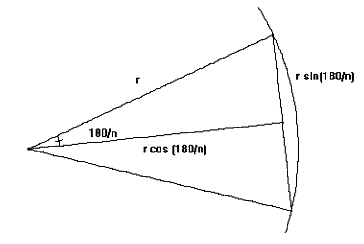
Innskreven mangekant
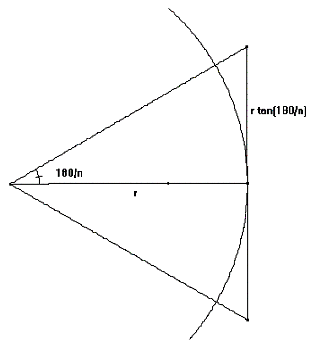
Omskreven mangekant
Ved hjelp av at

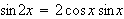 får vi da at arealene av disse mangekantene er
får vi da at arealene av disse mangekantene er
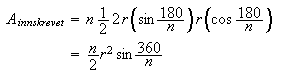
og
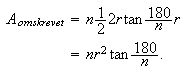
Arealet til sirkelen må ligge mellom disse to verdiene, altså
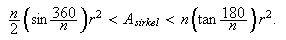
Hadde vi visst at sirkelens areal var gitt ved

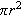 kunne vi videre funnet en tilnærming for
kunne vi videre funnet en tilnærming for

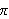 ved
ved
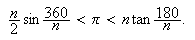
Da kan vi bestemme

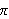 så nøyaktig vi vil (og har tid til) ved å øke
så nøyaktig vi vil (og har tid til) ved å øke

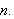 Som vi ser bygger vårt integralbegrep egentlig på nø yaktig
samme ide som Arkimedes' arealberegning.
Som vi ser bygger vårt integralbegrep egentlig på nø yaktig
samme ide som Arkimedes' arealberegning.
I [TL1, s.339] er det forresten en fin konklusjon med et forslag til hvordan
studenter skal forstå integralbegrepet:
''Hva blir så konklusjonen på dette avsnittet? At man bør tenke
på integralet på to forskjellige måter: Når det gjelder
den teoretiske definisjonen og de praktiske anvendelsene bør man tenke
på integralet som en grense av trappesummer, men når det gjelder
utregningen av integraler, er det mye mer effektiv å tenke
på antiderivasjon. Analysens fundamentalteorem sier at disse to
tenkemåtene stemmer overens.''
Konvergensbegrepet
Begrepene uendelig og
konvergens viser seg erfaringsmessig å være
tunge å fordøye for skoleelever. Fourierrekker viste seg
å være en morsom måte for elever (på 2MX-nivå)
å få rekkebegrepet innført på. Igjen er det Fouriers aller
første og aller enkleste eksempel som er et flott eksempel med gode og
pedagogiske poenger. Vi minner om trappefunksjonen fra kapittel 1, der vi
på intervallet

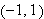 kan skrive
kan skrive
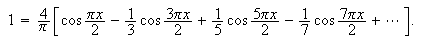
I
en 2MX-klasse brukte vi denne rekka for å eksperimentere litt med
kalkulator samtidig som vi skulle få en smaksprøve
på konvergensbegrepet. Følger av funksjoner er selvfølgelig
ikke pensum, og vi nevnte ikke noe om hvordan man skulle finne koeffisientene
(integralbegrepet innføres jo ikke før i 3MX). Elever i
videregående skoler i dag har tilgjengelig grafisk kalkulator, og det er
lett å justere hvor mange ledd som skal tegnes i summen. Elevene fikk
altså trent seg i mange aspekter ved å plotte partialsummer
på kalkulatoren.
-
De fikk oppgitt de første ledd i rekka og skulle gjette de fø lgende
selv - trening i å se mønster og strukturer.
-
De forsøkte å plotte partialsummene både ved å skrive inn
ledd for ledd, og senere ved å bruke summe-notasjonen
på kalkulatoren - ren mekanisk trening i bruk av hjelpemidler.
-
Man kunne observere hvordan man kunne legge sammen funksjoner, der man hadde
forskjellige frekvenser i cosinus-leddene, for å produsere andre
funksjoner - undersøke summer av funksjoner.
-
Man så at summene nærmet seg en trappefunksjon, og til og med Gibbs
fenomen kunne observeres etterhvert. Noen få elevene ble faktisk veldig
interessert i dette og begynte å studere vanskelige summer av (spesielt
trigonometriske) funksjoner på egen hånd. Ikke dårlig i 2MX!
Det virket iallfall som om elevene kunne ane viktigheten av uendelig-begrepet,
og spørsmålene de stilte skulle tyde på at de hadde
fått med seg flere viktige poeng:
Her ser vi også en måte å gripe fatt i pedagogiske virkemidler,
som dette å ''getting involved'' som [JM] nevner. Utforskning av
egenskaper til funksjoner og kurver er et av områdene der
IKT-verktøy og kalkulatorer er fint å anvende.
Anbefalt litteratur
Avslutningsvis vil vi nevne et par bøker som kan anbefales for videre
lesning.
-
Et prosjekt ved Transnational college of LEX har resultert i utgivelsen av
boken Who is Fourier? Her har man brukt
Fourieranalysen som utgangspunkt for å oppnå grunnlag for
å analysere stemmebruk. Under dette prosjektet, som man kalte
The Fourier adventure, handler det like mye om
læringsprosessen som om Fourier og hans matematikk. Etterhvert som man
kom lenger inn i Fourieranalysen åpenbarte det seg nye aspekter som
elevene kunne studere. Blant temane finner vi egenskaper ved trigonometriske
funksjoner, derivasjon for å finne fart og akselerasjon til objekter,
integrasjon for å finne tilbakelagt distanse for et objekt, komplekse
tall, eksponensialfunksjonen, vektorer m.m. De vanskeligste temaene i
forbindelse med konvergens og intrikate deler av bevisene er naturlig nok
utelatt. Elevmassen dette er myntet på tilsvarer ungdomsskole -
videregående skole, og et av poengene var også å bruke
matematikk som et internasjonalt språk. Kanskje kunne et tilsvarende tema
vært velegnet for valgfag i matematikk i den norske videregående
skole også?
-
TWK T.W. Körners bok, Fourier analysis, er
kanskje ikke så elementær som forfatteren vil ha det til, men er
veldig omfangsrik. I tillegg til å ta for seg favoritter som
punktvis/uniform konvergens, diff.likninger og Fouriertransformasjoner ser han
også på anvendelser som random walk, måling av stjerner, den
trans-atlantiske kabelen, gruppeteori m.m. Som han sier selv, boken er et
''butikkvindu for noen av ideene, teknikkene og elegante resultatene i
Fourieranalyse.''
-
I A radical approach to real analysis presenterer D.M.
Bressoud en del Fourieranalyse til å illustrere utviklingen av analysen.
Forfatteren bruker dataprogrammet Mathematica en hel
del for å illustrere resultater i analysen, og det er også mange
oppgaver som er tilrettelagt for arbeid på data-salen. Det gjør
boken veldig godt egnet både for egenstudium og til bruk ved høyere
utdanning, spesielt der man har anledning til å ta i bruk litt
alternative undervisningsformer.
-
Til sist nevnes J. Peetres artikkel om Fouriers oppdagelser og utviklingen av
Fourieranalysen, [JP]. En engelsk versjon av denne kan også lastes ned
fra Internett på adressen
http://www.maths.lth.se/matematiklu/personal/jaak/fourierseries,b.ps .
Dataverktøy
En del dataverktøy har blitt brukt i denne oppgaven, og noen kan
også anbefales brukt i skolen:
-
Graf-X-pert - Dette programmet er utviklet av Jostein
Våge (NTNU), spesielt beregnet til bruk i undervisningen. Programmet gir
læreren et interaktivt verktøy, som kan brukes til å lette
innføringen av begreper i matematikkundervisningen. At eleven aktiviseres
er en essensiell del av ideen.
Hovedfunksjonen er å illustrere ideen bak bestemte integraler, men man
kan også tilpasse kurver til gitte datasett. Elevene kan eksperimentere
med grafer og bruke det til å løse ligninger og ligningssett. Videre
kan man illustrere hvordan en sekant nærmer seg tangenten til grafen i et
bestemt punkt.
-
Cabri - Dette programmet eksisterer i flere ulike
versjoner, både for datamaskiner og for kalkulatorer. Noe av vitsen er
kanskje borte ved å bruke et program til å tegne geometriske figurer
på en kalkulator, men på en datamaskin kan man utvide
funksjonaliteten ved å lage makroer, og interaktive demonstrasjoner for
å illustrere begreper.
-
Scientific Workplace - Dette programmet eksisterer
også i flere versjoner, både som en ren matematisk tekstbehandler
(da under navnet Scientific Word), og som en fullblods
arbeidsstasjon, der man kan gjøre beregninger ved hjelp av en innbygd
MAPLE-motor. Til bruk i skolen har utviklerne supplert med et gratis
leseprogram, som elever kan laste ned for å kunne lese og skrive ut
matematiske dokumenter lagd i Scientific Workplace. Fra versjon 4.0 og utover
er også publisering på Internett gjort lettere.
Litteratur
| \lbrack S/Ø] |
Sandvold, K.E./Øgrim, S.: 2MN |
|
Gyldendal norsk forlag (1983); ISBN: 82-05-14385-4 |
| \lbrack JM] |
Mason, J.: Thinking mathematically |
|
Addison Wesley Publishing Company (1982); ISBN: 0201102382 |
| \lbrack TL2] |
Lindstrøm, T.: Tilnærming til
integralbegrepet |
|
Artikkel i ''Nye og gamle emner i matematikk'' |
|
Hefte utgitt i fb.m. Faglig-pedagogisk dag 19.11.1999 |
| \lbrack TL1] |
Lindstrøm, T.: Kalkulus |
|
Universitetsforlaget AS (1995); ISBN: 82-00-22472-4 |
| \lbrack LEX] |
Transnational College of LEX: Who is Fourier? |
|
Language research foundation (2000); ISBN: 0-9643504-0-8 |
| \lbrack TWK] |
Körner, T.W.: Fourier Analysis |
|
Cambridge university press (1988); ISBN: 0-521-25120-6 |
| \lbrack DMB] |
Bressoud, D.M.: A radical approach to real
analysis |
|
The Mathematical Association of America (1993); ISBN: 0883857014 |
| \lbrack JP] |
Peetre, J.: Om Fouriers upptäckt av Fourierserier og
Fourierintegraler |
|
NORMAT 50, 2002 |
This document created by Scientific WorkPlace 4.0.
Neste: Divergensteoremet

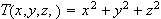 .
Hvordan skal man kunne assimilere et slikt begrep hvis man er fastlåst
til sine gamle begreper, og samtidig skulle tro man er i stand til
å tegne en slik funksjon? Og hvem fikk vel høre i 2MX / 3MX at det
fins funksjoner av typen
.
Hvordan skal man kunne assimilere et slikt begrep hvis man er fastlåst
til sine gamle begreper, og samtidig skulle tro man er i stand til
å tegne en slik funksjon? Og hvem fikk vel høre i 2MX / 3MX at det
fins funksjoner av typen

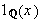 som nevnt tidligere? Man kan vel innvende at slike funksjoner ikke bør
stå sæ rlig sentralt i videregående skoles matematikk-pensum,
men det må vel ligge et poeng i å vite at de fins? I alle fall burde
lærerne være klar over situasjonen.
som nevnt tidligere? Man kan vel innvende at slike funksjoner ikke bør
stå sæ rlig sentralt i videregående skoles matematikk-pensum,
men det må vel ligge et poeng i å vite at de fins? I alle fall burde
lærerne være klar over situasjonen.