
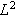 -funksjoner)
fant han heller en annen type konvergens som kunne benyttes.
-funksjoner)
fant han heller en annen type konvergens som kunne benyttes.
Denne seksjonen tar for seg resultater parallelle til de i forrige seksjon, men representerer samtidig en slags utvidelse av det konvergensbegrepet Dirichlet brukte. Vi skal ikke være så omstendelige som i forrige kapittel, og bruker nå den komplekse utgaven av Fourierrekkene. At Fejérs teorem er et viktig resultat ser vi av et utsagn fra [TWK], der forfatteren mener dette er essensen i Fourieranalysen og en forståelse av Fejérs teorem fører til at ''the reader may browse freely through this book...''.
Fejér kjente til problemet om at ikke alle funksjoner kunne utvikles i
Fourierrekker som konvergerte punktvis mot denne funksjonen. I stedet for
å finne den best egnede funksjonsklassen (som Lebesgue gjorde med sine

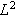 -funksjoner)
fant han heller en annen type konvergens som kunne benyttes.
-funksjoner)
fant han heller en annen type konvergens som kunne benyttes.
Vi så i forrige kapittel at det tok tid før problemet med punktvis konvergens av Fourierrekker ble løst. Faktisk har Kolmogorov Note_1 vist at Fourierrekka til en integrerbar funksjon kan divergere overalt [B/N/B, s.211ff].
Fejér oppdaget i 1899 (i en alder av 19 år!) at selv om en
følge ikke oppførte seg så pent i seg selv, så kunne
middelverdien av partialsummene til følgen gjøre det.
Altså; selv om ikke følgen av partialsummer
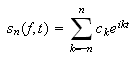
konvergerer så kan følgen av middelverdier av partialsummene
konvergere (på en eller annen måte).
For å se hva det dreier seg om, kan vi se på følgende resultat:
Hvis

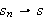 så vil
også
så vil
også 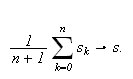
Siden følgen

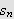 konvergerer mot
konvergerer mot

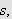 så kan vi til gitt
så kan vi til gitt

 finne
finne

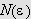 slik at vi for
slik at vi for

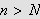 har
har

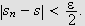 For
For

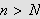 har vi da
har vi da
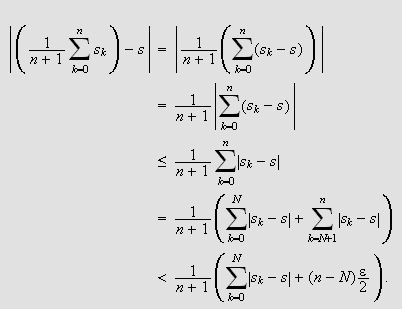
Nå er summen

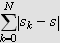 en konstant, la oss si
en konstant, la oss si

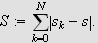 Vi kan da velge en
Vi kan da velge en

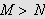 slik at
slik at

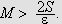 For
For

 vil da
vil da

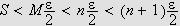 .
Da får vi
.
Da får vi
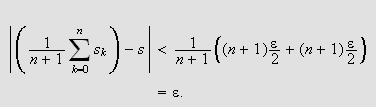
Det vil si, når

 eksisterer, eksisterer
også
eksisterer, eksisterer
også 
 , og de har samme verdi.
, og de har samme verdi.
Motsatt har vi ikke det samme resultatet, noe følgende enkle eksempel demonstrerer.
Se på følgen

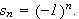 Da vil opplagt ikke
Da vil opplagt ikke

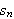 konvergere, siden den alternerer mellom verdiene
konvergere, siden den alternerer mellom verdiene

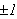 .
Vi har
.
Vi har
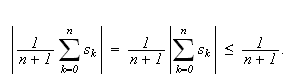
Siden følgen

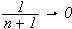 ,
vil
også
,
vil
også 
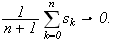 Følgen av middelverdier av partialsummene konvergerer altså, selv om
følgen opprinnelig ikke gjø r det.
Følgen av middelverdier av partialsummene konvergerer altså, selv om
følgen opprinnelig ikke gjø r det.
Dette var altså hovedidèen til Fejér, en enkel observasjon, men
med utstrakt anvendbarhet. Vi husker fra forrige kapittel at Dirichlet-kjernen
var definert ved
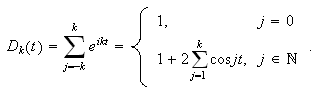
På denne måten kunne Dirichlet skrive partialsummen i Fourierrekka
som
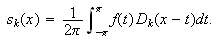
Fejér brukte en tilsvarende omskriving, der han tok middelverdien av de

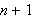 første partialsummene. Middelverdien av partialsummene har også sitt
eget navn:
første partialsummene. Middelverdien av partialsummene har også sitt
eget navn:
Vi skriver middelet av de

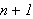 første partialsummene som
første partialsummene som
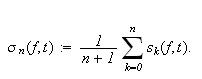
Dette kalles også Cesàro-middelet
Note_2 av Fourierrekka,
og metoden med å summere i utgangspunktet divergente rekker på denne
må ten, kalles Cesàro-summasjon.
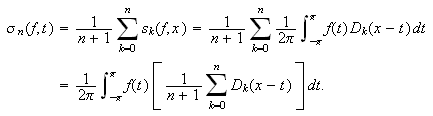
Vi bruker så følgende definisjon:
\underline{Fejér-kjernen
K
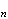 }
av orden n defineres ved
}
av orden n defineres ved
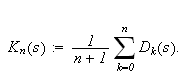
Det er også en annen måte å skrive
Fejér-kjernen Note_3
på. En omforming av Cesaro-summen gir
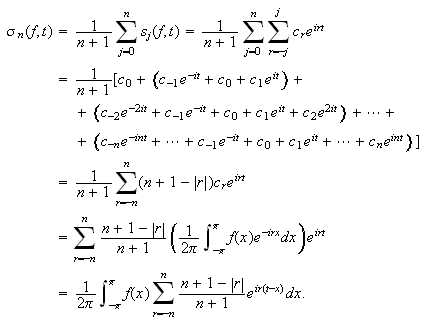
Her innfører vi da den andre skrivemåten for
Fejér-kjernen:
\underline{Fejér-kjernen

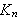 }
av orden
}
av orden

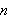 er gitt ved
er gitt ved
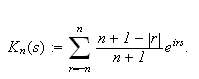
Vi kan da skrive () slik:
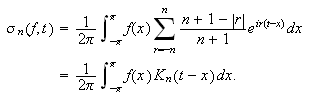
Denne er symmetrisk i den forstand at vi kan skrive
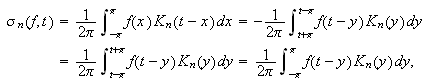
siden både

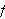 og
og

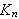 er
er

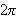 -periodiske.
Fejérs teorem sier at Cesaro-summen
-periodiske.
Fejérs teorem sier at Cesaro-summen

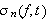 konvergerer (på en eller annen måte) mot
konvergerer (på en eller annen måte) mot

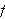 ,
uavhengig av om
,
uavhengig av om

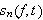 gjør det.
gjør det.
La oss danne oss et bilde av hvordan

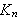 ser ut.
ser ut.

Fejér-kjernen

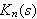 for
for

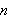 -verdier
2,4 og 8.
-verdier
2,4 og 8.
Noen egenskaper ved

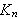 er oppsummert i følgende lemma.
er oppsummert i følgende lemma.
(ii)

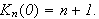
(iii)

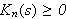 for alle
for alle

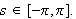
(iv)

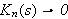 uniformt utenfor
uniformt utenfor

![$[-\delta ,\delta ]$](fejer__67.png) for hver fastholdt
for hver fastholdt

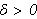 når
når

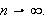
(v)

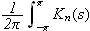

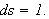

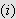 I forrige kapittel viste vi at Dirichlet-kjernen
I forrige kapittel viste vi at Dirichlet-kjernen

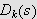 kan skrives
kan skrives
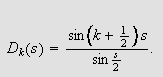
Siden Féjer-kjernen

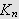 kan skrives
kan skrives
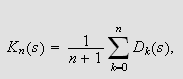
så er
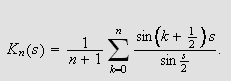
Da får vi
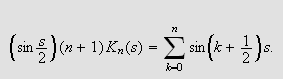
Siden

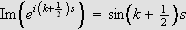 får vi
får vi
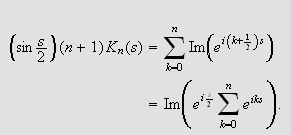
Vi bruker nå summeformelen for en geometrisk
rekke:
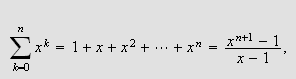
når

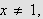 for å få
for å få
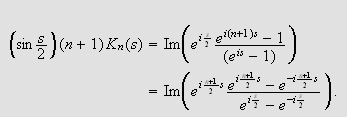
Minner nå om formelen
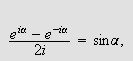
som gir
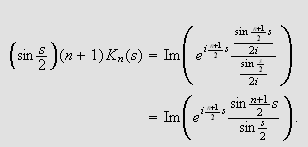
Vi vet at

 når
når

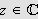 og
og

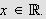 Derfor er
Derfor er
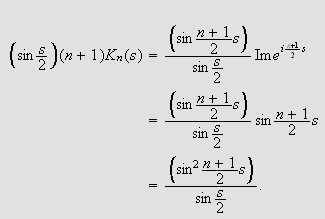
Altså kan

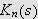 skrives
skrives
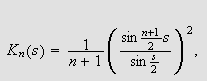
som
ønsket


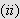 Vi vet at summen av de
Vi vet at summen av de

 første oddetallene er
første oddetallene er

 Videre har vi fra lemma 19 at
Videre har vi fra lemma 19 at

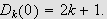 Fra () følger det da at
Fra () følger det da at
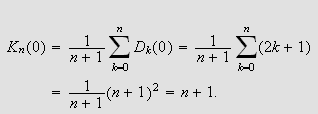

 Innlysende, siden Fejér-kjernen er kvadratet av et reellt uttrykk
multiplisert med en positiv konstant (se (i)).
Innlysende, siden Fejér-kjernen er kvadratet av et reellt uttrykk
multiplisert med en positiv konstant (se (i)).

 Vi vet at
Vi vet at

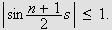 Fiksér en
Fiksér en

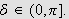 Når
Når

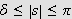 så er
så er

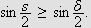 Vi har da for
Vi har da for

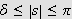 at
at
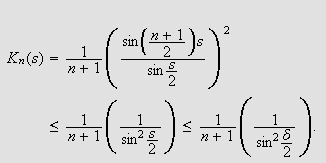
Til gitt

 kan vi da finne et naturlig tall
kan vi da finne et naturlig tall

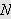 slik at
slik at

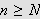 medfører
medfører
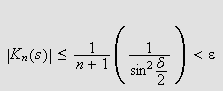
for alle

 med
med

 Med andre ord,
Med andre ord,

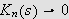 uniformt utenfor
uniformt utenfor

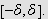

 En enkel antiderivasjon gir at
En enkel antiderivasjon gir at

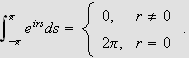 Da følger det fra definisjonen av Fejér-kjernen at
Da følger det fra definisjonen av Fejér-kjernen at

Og alt er bevist.
Ved hjelp av Lemma 31 kan vi nå bevise Fejérs teorem.
[TWK, s.6]

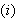 Hvis
Hvis

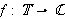 er Riemann-integrerbar og kontinuerlig i punktet
er Riemann-integrerbar og kontinuerlig i punktet

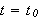 så vil
så vil
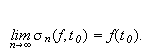

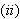 Hvis
Hvis

 er kontinuerlig så vil
er kontinuerlig så vil
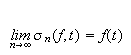
\underline{uniformt}.

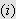 Siden
Siden

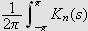

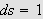 så er
så er

Vi har da
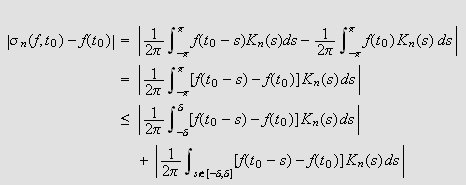
Sett
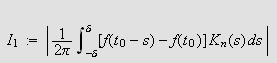
og
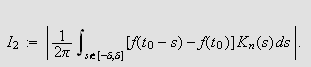
La
nå 
 være gitt.
være gitt.
Vi ser først
på 
 Siden
Siden

 er kontinuerlig i
er kontinuerlig i

 kan vi finne
kan vi finne

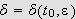 s.a.
s.a.

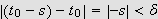 medfører
medfører

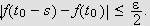 Fiksér en slik
Fiksér en slik

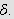 Da får vi
Da får vi
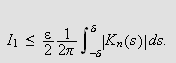
Vi vet, siden

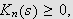 at
at

Det vil si,

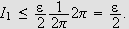
Vi ser
så på 
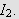 Vi antok at
Vi antok at

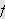 er Riemann-integrerbar og den må derfor være begrenset. Da kan vi
sette
er Riemann-integrerbar og den må derfor være begrenset. Da kan vi
sette

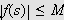 ,
og da er spesielt
,
og da er spesielt

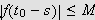 og
og

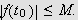 Det følger at
Det følger at

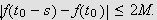
Altså har vi for det andre integralet at
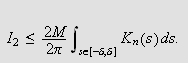
På grunn av egenskap

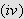 i lemma 31 kan vi finne et naturlig tall
i lemma 31 kan vi finne et naturlig tall

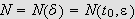 s.a.
s.a.

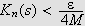 for alle
for alle

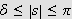 når
når

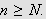 Da får vi
Da får vi

Dette gir
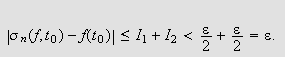

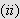 Som over har vi
Som over har vi
La

 være gitt. Siden vi nå har antatt
være gitt. Siden vi nå har antatt

 kontinuerlig over hele
kontinuerlig over hele

 kan vi finne
kan vi finne

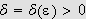 slik at
slik at

 for alle
for alle

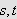 s.a.
s.a.

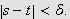 Fiksér en slik
Fiksér en slik

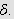 Siden
Siden

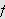 er kontinuerlig
på
er kontinuerlig
på 
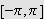 har vi
har vi

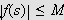 for alle
for alle

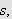 slik at
slik at

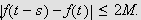 Da er
Da er
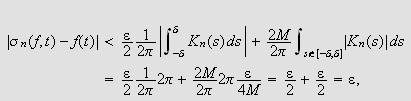
som påstått.
| \lbrack TWK] | Körner, T.W.: Fourier Analysis |
| Cambridge university press (1988); ISBN: 0-521-25120-6 | |
| \lbrack B/N/B] | Bachman, G./Narici, L./Beckenstein, E.: Fourier and Wavelet analysis |
| Springer Verlag New York 2000. ISBN: 0-387-98899-8 |
Neste: Fourierintegraler
Forrige: Fourierrekker
This document created by Scientific WorkPlace 4.0.