
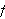 med en rekke bestående av cosinusledd med forskjellige amplituder og
frekvenser. Vanskeligheten lå altså i når
vi hadde lov til å gjøre dette.
med en rekke bestående av cosinusledd med forskjellige amplituder og
frekvenser. Vanskeligheten lå altså i når
vi hadde lov til å gjøre dette.
''Differensiallikningene for varmeteori uttrykker de mest generelle forutsetninger og reduserer de fysiske spørsmål til rene analytiske problemer. Dette er den riktige angrepsmåte for teori.''
(Joseph Fourier [JF, s.6])
Vi så i første kapittel på den første idéen Fourier
beskriver i avhandlingene sine, nemlig hvordan en påsatt temperatur
stabiliserer seg over en semi-uendelig plate. Resonnementet endte opp med at
man ønsket å representere en funksjon

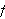 med en rekke bestående av cosinusledd med forskjellige amplituder og
frekvenser. Vanskeligheten lå altså i når
vi hadde lov til å gjøre dette.
med en rekke bestående av cosinusledd med forskjellige amplituder og
frekvenser. Vanskeligheten lå altså i når
vi hadde lov til å gjøre dette.
Siden de trigonometriske leddene er periodiske vil også denne
representasjonen være periodisk, ofte med hensyn på tid (derfor er
variablen

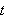 mye brukt her). Dette innebærer at vi må lage en periodisk utvidelse
av funksjonen vi vil finne Fourierrekke til. Men vi er altså bare
interesserte i å få utviklingen til å ''likne
på
mye brukt her). Dette innebærer at vi må lage en periodisk utvidelse
av funksjonen vi vil finne Fourierrekke til. Men vi er altså bare
interesserte i å få utviklingen til å ''likne
på 
![]() på et bestemt intervall, hva som skjer utenfor dette intervallet trenger
vi ikke å tenke på. Generelt har vi følgende definisjon for en
periodisk funksjon:
på et bestemt intervall, hva som skjer utenfor dette intervallet trenger
vi ikke å tenke på. Generelt har vi følgende definisjon for en
periodisk funksjon:
En funksjon

![]()

![]() kalles
\underline{periodisk} hvis det fins en
kalles
\underline{periodisk} hvis det fins en

![]() slik at
slik at

![]() for alle
for alle

![]() .
Vi kaller da
.
Vi kaller da

![]() \underline{en periode} til
\underline{en periode} til

Merk at perioden ikke er unik. Hvis

![]() er en periode vil
også
er en periode vil
også 
![]()

![]() være perioder. Legg også merke til at en vilkårlig
være perioder. Legg også merke til at en vilkårlig

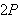 -periodisk
funksjon
-periodisk
funksjon

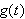 kan gjøres
kan gjøres

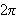 -periodisk
ved en skalering. Hvis
-periodisk
ved en skalering. Hvis

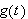 er
er

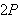 -periodisk
så vil
-periodisk
så vil

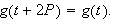 Sett
Sett

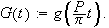 Denne vil da være
Denne vil da være

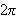 -periodisk,
siden
-periodisk,
siden
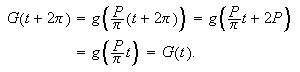
Dette fører til at vi kan konsentrere teorien omkring intervallet

 ,
da et variabelskifte senere vil kunne omforme problemer definert på andre
intervaller til det kjente tilfellet. Andre begreper vi støter på i
Fourierteorien er følgende:
,
da et variabelskifte senere vil kunne omforme problemer definert på andre
intervaller til det kjente tilfellet. Andre begreper vi støter på i
Fourierteorien er følgende:
Et \underline{trigonometrisk polynom} er en funksjon på formen
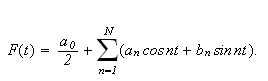
Vi kan også bruke en kompleks variant, ved å benytte at

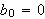 ,
,

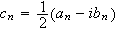 og
og

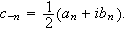 Da får vi
Da får vi
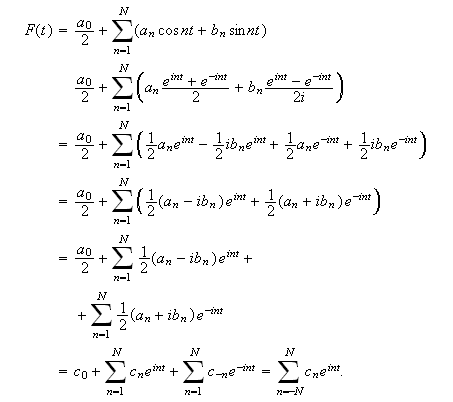
En \underline{trigonometrisk rekke} har formen
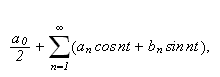
eller, på kompleks form,
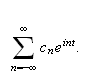
Den komplekse formen har en del regnetekniske fordeler og er også mer elegant. Derfor er den mest brukt i mer avansert litteratur. Da man kanskje ikke er kjent med komplekse tall vil nok den reelle varianten være lettere for de fleste ved første møte med Fourierteori. Vi skal i denne seksjonen stort sett holde oss til denne mest kjente notasjonen.
Generelt definerer vi Fourierrekker slik:
En (reell) \underline{Fourierrekke} tilhørende en funksjon

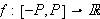 har generelt formen
har generelt formen
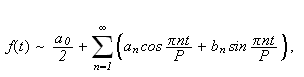
der
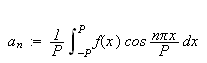
og
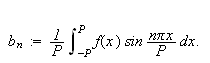
Disse kalles \underline{Fourierkoeffisientene}.
Thildetegnet i definisjonen kan for eksempel leses ''...har Fourierrekke...''.
Vi har i denne definisjonen brukt den generelle perioden

![]() Som bemerket ovenfor er det mest vanlige
intervallet
Som bemerket ovenfor er det mest vanlige
intervallet 
![]() Vi skal bruke en vanlig konvensjon, nemlig å kalle definisjonsmengden til
Vi skal bruke en vanlig konvensjon, nemlig å kalle definisjonsmengden til

 -periodiske
funksjoner for
-periodiske
funksjoner for

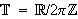 ,
eller sirkelen, om man vil. Andre intervaller som ofte er brukt er
,
eller sirkelen, om man vil. Andre intervaller som ofte er brukt er

![$[0,2\pi ]$](rekker__39.png) ,
,

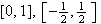 og
og

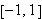 .
Vi vil i det etterfølgende bruke
.
Vi vil i det etterfølgende bruke

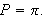 Da vil Fourierrekka kunne skrives på den mer kjente formen
Da vil Fourierrekka kunne skrives på den mer kjente formen
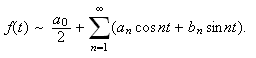
Leddet

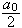 kan muligens se litt merkelig ut, men grunnen til at dette brukes i stedet for
kan muligens se litt merkelig ut, men grunnen til at dette brukes i stedet for

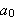 er at vi i () kan oppnå en og samme formel for
samtlige
er at vi i () kan oppnå en og samme formel for
samtlige

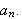
Men hvorfor var det ikke noen sinusledd i Fouriers rekkeutvikling i problemet
med varmeledning på platen? Ser vi på definisjonen av

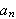 og
og

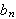 ser vi at koeffisientene
ser vi at koeffisientene

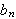 vil bli 0 for en like funksjon (produktet av en like og en odde funksjon er
selv odde).
vil bli 0 for en like funksjon (produktet av en like og en odde funksjon er
selv odde).
Det er viktig å skille mellom Fourierrekke og konvergent trigonometrisk rekke.
En Fourierrekke er en trigonometrisk rekke knyttet til en bestemt funksjon. Denne rekka kan være konvergent (på en eller annen måte - vi husker fra forrige kapittel at vi har flere former for konvergens) eller den kan være divergent.
På den annen side kan vi ha konvergente trigonometriske rekker som ikke
er Fourierrekker. Et standard eksempel her er

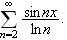 Denne rekka konvergerer punktvis for
Denne rekka konvergerer punktvis for

 men det fins ingen integrerbar funksjon som har denne rekka som Fourierrekke
[PRA, s.80]. En kuriositet i denne forbindelse er at
men det fins ingen integrerbar funksjon som har denne rekka som Fourierrekke
[PRA, s.80]. En kuriositet i denne forbindelse er at

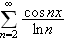 faktisk er en Fourierrekke! Dette er beskrevet i [KRS,
s.516], og her kommer også resultater fra Abel inn. Imidlertid er enhver
uniformt konvergent trigonometrisk rekke også en
Fourierrekke (se f.eks. [B/N/B, s.202]).
faktisk er en Fourierrekke! Dette er beskrevet i [KRS,
s.516], og her kommer også resultater fra Abel inn. Imidlertid er enhver
uniformt konvergent trigonometrisk rekke også en
Fourierrekke (se f.eks. [B/N/B, s.202]).
Det har hele tiden ligget i kortene at man ønsker å erstatte

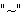 med
med

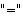 slik at denne rekken kan benyttes ''i stedet'' for funksjonen, og det var jo
også dette konvergensspørsmålet som opptok Fouriers
evalueringskomite. Vi skal senere se at klassen av funksjoner
slik at denne rekken kan benyttes ''i stedet'' for funksjonen, og det var jo
også dette konvergensspørsmålet som opptok Fouriers
evalueringskomite. Vi skal senere se at klassen av funksjoner

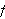 som kan utvikles i Fourierrekker som konvergerer mot
som kan utvikles i Fourierrekker som konvergerer mot

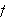 (på en eller annen måte) er stor, men inkluderer likevel ikke alle
funksjoner.
(på en eller annen måte) er stor, men inkluderer likevel ikke alle
funksjoner.
Hvis vi antar rekka i () konvergerer uniformt mot

 kan vi finne formler for
kan vi finne formler for

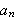 og
og

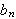 .
Man kommer ikke unna litt regning. Vi skal for enkelthets skyld bruke perioden
.
Man kommer ikke unna litt regning. Vi skal for enkelthets skyld bruke perioden

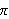 og minner først om formler for cosinus til sum og differens til vinkler:
og minner først om formler for cosinus til sum og differens til vinkler:
![]()
og
![]()
Vi kan da sette opp
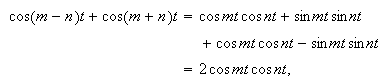
slik at vi får identiteten
![]()
På tilsvarende måter får vi identitetene
![]()
og
![]()
Disse gir oss for

![]() at
at
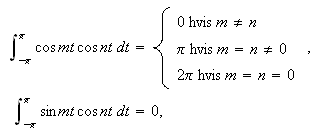
og
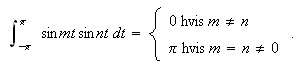
Vi nøyer oss med å vise (). Hvis

 får vi
får vi
![]()
Hvis

 blir integralet
blir integralet
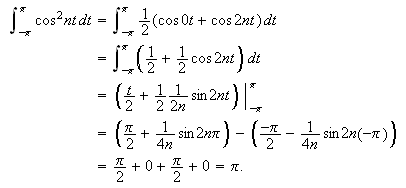
Og til slutt hvis

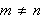 får vi:
får vi:
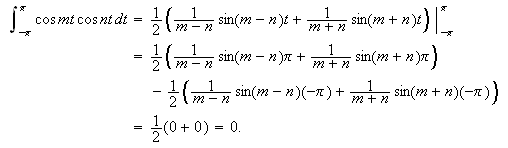
Vi antok uniform konvergens av rekka, så la oss nå sette
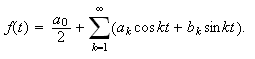
I forrige kapittel viste vi at en uniformt konvergent følge kan
integreres ledd for ledd, det vil si at

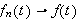 uniformt
på
uniformt
på 
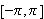 medfører at
medfører at
![]()
I vårt tilfelle består følgen av partialsummer i Fourierrekka,
se på
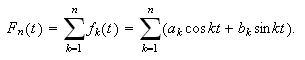
Antakelsen vår er derfor at

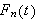 er en følge som konvergerer uniformt mot summen til rekka,
er en følge som konvergerer uniformt mot summen til rekka,

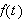 .
Vi har altså eksempelvis at
.
Vi har altså eksempelvis at
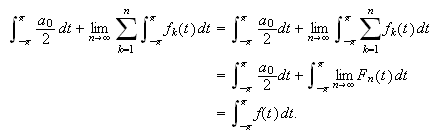
Multipliserer vi () med

![]() har vi fortsatt uniform konvergens. Vi kan da integrere ledd for ledd (se
også f.eks. [PRA, s.60f]).
har vi fortsatt uniform konvergens. Vi kan da integrere ledd for ledd (se
også f.eks. [PRA, s.60f]).
Integrerer vi begge sider fra

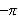 til
til

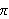 får vi for
får vi for

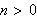 at
at

De to siste likhetene fulgte av () og (). På samme måte får vi
![]()
Oppsummert har vi at Fourierkoeffisientene er gitt ved
![]()
og
![]()
som i definisjonen.
Vi annonserte at kompleks notasjon kan forenkle arbeidet med Fourierrekker. Vi
får
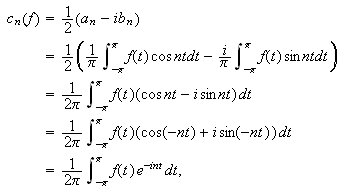
slik at vi kan gi følgende definisjon av Fourierkoeffisienten:
Den \underline{komplekse Fourierkoeffisienten

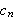 }
er gitt ved
}
er gitt ved
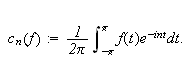
Fourierrekka har da formen
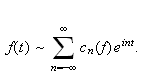
Når det ikke er tvil om hvilken funksjon det er snakk om, droppes som
regel notasjonen

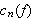 og man skriver
og man skriver

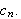
Vi skal i denne seksjonen gi et bevis for at Fourierrekka til en funksjon

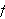 konvergerer punktvis mot
konvergerer punktvis mot

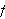 under visse
vilkår
under visse
vilkår
![]() Etter de nevnte mislykkede forsøk fra Fourier,
Gauss Note_1 og Cauchy var det
altså Dirichlet som kom med første gyldige resultat angående
punktvis konvergens av Fourierrekker. Han hadde riktignok en mistanke om at
hans teorem holdt for en større klasse funksjoner enn han hadde studert,
men klarte ikke å vise det. Vi fikk senere, med
Jordan Note_2 , en slik utvidelse av
funksjonsklassen som tillater Fourierrepresentasjoner. Her ble begrepet
begrenset variasjon introdusert. La oss nå i
fø rste omgang se på hva Dirichlet gjorde. I neste kapittel skal vi
også se på Fejers Note_3
bevis med en annen type konvergens. Dirichlet introduserte notasjonen
Etter de nevnte mislykkede forsøk fra Fourier,
Gauss Note_1 og Cauchy var det
altså Dirichlet som kom med første gyldige resultat angående
punktvis konvergens av Fourierrekker. Han hadde riktignok en mistanke om at
hans teorem holdt for en større klasse funksjoner enn han hadde studert,
men klarte ikke å vise det. Vi fikk senere, med
Jordan Note_2 , en slik utvidelse av
funksjonsklassen som tillater Fourierrepresentasjoner. Her ble begrepet
begrenset variasjon introdusert. La oss nå i
fø rste omgang se på hva Dirichlet gjorde. I neste kapittel skal vi
også se på Fejers Note_3
bevis med en annen type konvergens. Dirichlet introduserte notasjonen

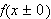 for å symbolisere høyre/venstre ensidige grenseverdi for
for å symbolisere høyre/venstre ensidige grenseverdi for

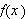 når vi nærmer oss
når vi nærmer oss

![]() Følgende variant har imidlertid blitt mer vanlig, sannsynligvis for
å unngå misforstå elser:
Følgende variant har imidlertid blitt mer vanlig, sannsynligvis for
å unngå misforstå elser:
Symbolet

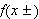 betyr høyre eller venstre ensidige grenseverdi for
betyr høyre eller venstre ensidige grenseverdi for

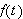 når vi nærmer oss punktet
når vi nærmer oss punktet

![]() Altså;
Altså;
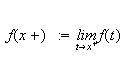
og
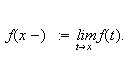
Vi skal i det etterfølgende bevise Dirichlets teorem, som lyder:
La

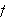 være
en begrenset, stykkevis kontinuerlig og stykkevis monoton funksjon
på
være
en begrenset, stykkevis kontinuerlig og stykkevis monoton funksjon
på

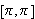 .
Anta at
.
Anta at

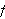 er
er

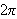 -periodisk
og at
-periodisk
og at

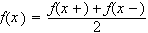 for
alle
for
alle

![]() Når
Når

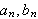 er
Fourierkoeffisientene til
er
Fourierkoeffisientene til

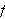 vil
rekka
vil
rekka
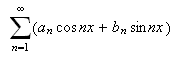
konvergere punktvis mot

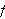 for
alle
for
alle

![]() Vi skriver da
Vi skriver da
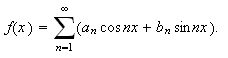
Vi minner om at stykkevis kontinuerlig betyr at

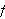 er kontinuerlig, bortsett fra i et endelig antall punkter. I tillegg
må
er kontinuerlig, bortsett fra i et endelig antall punkter. I tillegg
må 
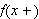 og
og

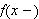 være endelig for alle
være endelig for alle

![]() Stykkevis monoton betyr at vi kan dele definisjonsmengden
Stykkevis monoton betyr at vi kan dele definisjonsmengden

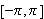 opp i intervaller der
opp i intervaller der

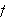 er monoton på hvert delintervall. Som vi ser er antakelsene om
er monoton på hvert delintervall. Som vi ser er antakelsene om

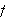 mange, og vi skal prøve å motivere disse underveis. Det kan kanskje
se ut som om kravet
mange, og vi skal prøve å motivere disse underveis. Det kan kanskje
se ut som om kravet

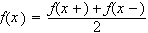 for alle
for alle

![]() er en veldig sterk antakelse, men for eksempel vil en kontinuerlig funksjon
oppfylle dette kravet. Strengt tatt trenger vi ikke
å anta dette, bare være oppmerksomme
på at grensen blir
er en veldig sterk antakelse, men for eksempel vil en kontinuerlig funksjon
oppfylle dette kravet. Strengt tatt trenger vi ikke
å anta dette, bare være oppmerksomme
på at grensen blir

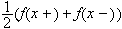 der
der

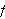 ikke er kontinuerlig (så lenge de andre forutsetningene i teoremet er
oppfyllt).
ikke er kontinuerlig (så lenge de andre forutsetningene i teoremet er
oppfyllt).
Dirichlet stilte på en måte problemstillingen på hodet.
Fourier, Cauchy og Gauss hadde startet med en funksjon og prøvde
å vise at man da klarte å finne

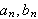 slik at Fourierrekka konvergerte. Dirichlet på den annen side sier i
teoremet at Fourierrekka allerede er der,
altså at vi har Fourierrekka til
slik at Fourierrekka konvergerte. Dirichlet på den annen side sier i
teoremet at Fourierrekka allerede er der,
altså at vi har Fourierrekka til

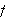 ,
men
,
men

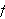 må tilhøre en viss funksjonsklasse (tilfredsstille visse krav) for
at rekka skal konvergere mot
må tilhøre en viss funksjonsklasse (tilfredsstille visse krav) for
at rekka skal konvergere mot

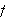 .
.
Når vi ønsker å vise at en rekke konvergerer er det som nevnt
det samme som å vise at følgen av partialsummer i rekka konvergerer.
Partialsummen til Fourierrekka til en funksjon er
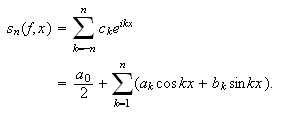
Vi skriver bare

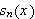 når det er underforstått hvilken funksjon det dreier seg om.
Dirichlet ønsket altså å vise at man til gitt
når det er underforstått hvilken funksjon det dreier seg om.
Dirichlet ønsket altså å vise at man til gitt

![]() og
og

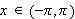 kan finne
kan finne

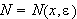 slik at
slik at

![]() medfører
medfører

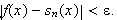 Vi ledes til å studere partialsummen til rekka, og det fins en
hensiktsmessig måte å skrive om denne på, nemlig via den
såkalte Dirichlet-kjernen.
Vi ledes til å studere partialsummen til rekka, og det fins en
hensiktsmessig måte å skrive om denne på, nemlig via den
såkalte Dirichlet-kjernen.
Partialsummene i Fourierrekka kan skrives som
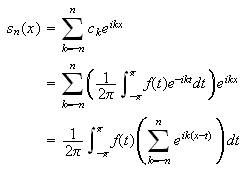
Her er det snakk om endelig summasjon, så bytte av integrasjon og
summasjon er tillatt. Se så på summer av en slik type som i
parantesen over,
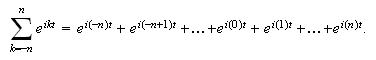
Med Eulers formel

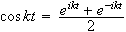 får vi
får vi
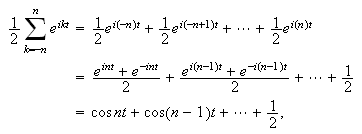
slik at
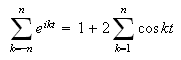
for

 Dermed kan vi gi følgende definisjon:
Dermed kan vi gi følgende definisjon:
\underline{Dirichlet-kjernen av orden

![]() }
er gitt ved
}
er gitt ved
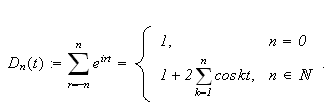
Altså har vi at partialsummen kan skrives som
![]()
Av dette ser vi at konvergens av Fourierrekker også dreier seg om
egenskaper ved

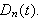 Noen typiske Dirichletkjerner ser slik ut (ø kende
Noen typiske Dirichletkjerner ser slik ut (ø kende

![]() gir høyere og spissere kurve):
gir høyere og spissere kurve):

Dirichlet-kjernen

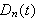 for
for

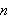 -verdiene
1,3 og 5.
-verdiene
1,3 og 5.
Noen egenskaper ved denne kjernen er oppsumert i følgende lemma:
(i) Definisjonen av

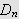 gir
gir
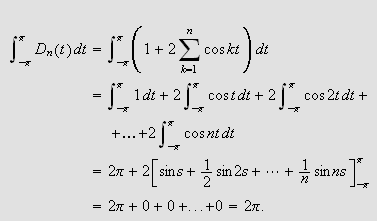
(ii) Formelen for sinus til sum og differens av vinkler,
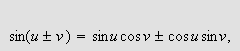
gir at
Da vil
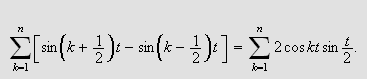
Summen på venstre side inneholder kansellerende ledd, så bare
første og siste ledd gjenstår, det vil si
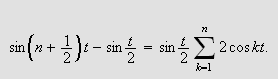
Dette gir at
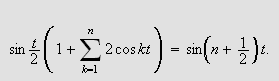
Siden

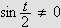 for
for

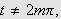

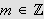 ,
så gir dette at
,
så gir dette at
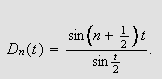
(iii) Direkte utregning gir

(iv) Definisjonen av Dirichletkjernen gir

Integrasjon ledd for ledd gir da
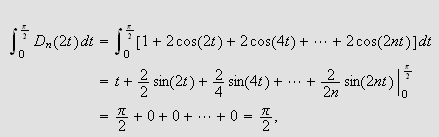
og alt er bevist.
Dirichlet brukte den vanlige reelle notasjonen når han regnet med Fourierrekker, så vi skal holde oss til den videre i dette avsnittet. Han måtte takle flere problemer som Fourier hadde støtt på, men kanskje ikke registrert vinteren 1807.
Vi skal se på beviset omtrent slik Dirichlet gjorde det ([DMB, s.219ff] og [B/N/B, s.188ff]). Dette beviset er velkjent i Fourierteorien og finnes i de fleste bøker om dette emnet.
For det første fikk man bruk for den originale definisjonen av
integralet. Som nevnt i forrige kapittel, måtte man gi en definisjon av
![]()
i de tilfeller der hvor man ikke kunne finne en antiderivert. Derfor må
tte man ha den første antagelsen:

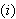 Funksjonen
Funksjonen

 må være
integrerbar.
må være
integrerbar.
Her menes det da integrerbar med hensyn på Cauchy-integralet (eller ekvivalent, Riemann-integralet).
Fra () har vi at

![]() 'te
partialsum kan skrives
'te
partialsum kan skrives
![]()
Dette integralet deler vi i to. I første del erstatter vi

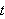 med
med

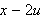 .
Da blir
.
Da blir

![]() Integrasjonsgrensene der
Integrasjonsgrensene der

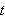 skal gå fra
skal gå fra

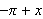 til
til

![]() blir da til at
blir da til at

![]() går fra
går fra

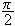 til
til

![]() (Vi bytter om på grensene i integrasjonen og skifter fortegn).
På grunn av symmetri ser vi også at
(Vi bytter om på grensene i integrasjonen og skifter fortegn).
På grunn av symmetri ser vi også at

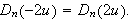 På tilsvarende måte settes i andre del
På tilsvarende måte settes i andre del

![]() Omskrivingen
Omskrivingen
![]()
kan vi foreta siden integranden er

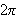 -periodisk.
Partialsummen kan da skrives
-periodisk.
Partialsummen kan da skrives
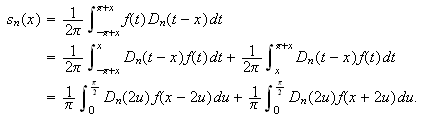
Fra definisjonen av

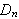 er det opplagt at
er det opplagt at

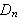 har periode
har periode

 og for at hele integranden skal være
og for at hele integranden skal være

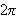 -periodisk
må vi sørge for at
også
-periodisk
må vi sørge for at
også 
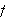 er det. Vi kan nemlig definere
er det. Vi kan nemlig definere

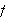 slik vi vil utenfor intervallet
slik vi vil utenfor intervallet

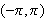 og derfor sette
og derfor sette

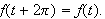 Herfra kommer altså neste antagelse:
Herfra kommer altså neste antagelse:

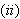 Vi
må ha at
Vi
må ha at

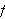 må være
må være

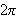 -periodisk.
-periodisk.
Vi setter i det følgende
![]()
og
![]()
Vi så allerede i kapittel 1 på en funksjon som ikke var kontinuerlig og det lå altså i problemets natur at man ønsket å finne Fourierrekker for funksjoner som ikke er kontinuerlige. Hva skjer med Fourierrekkene i diskontinuitetspunkter? Dirichlet løste også dette problemet med sin tredje antakelse:
(iii) Dersom

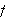 ikke
er kontinuerlig så må funksjonsverdien i diskontinuitetspunktene
være middelverdien av grensen fra venstre og grensen fra
høyre.
ikke
er kontinuerlig så må funksjonsverdien i diskontinuitetspunktene
være middelverdien av grensen fra venstre og grensen fra
høyre.
Vi skal senere komme fram til at
![]()
La oss tenke oss hvordan Dirichlet muligens gikk fram for å komme fram
til denne betingelsen. Dette skal gjøres presist i beviset for Dirichlets
teorem. Det første vi kan merke oss er at

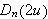 har sitt første nullpunktet til høyre når
har sitt første nullpunktet til høyre når

![]() det vil si, for
det vil si, for

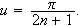 Se
nå på
Se
nå på 
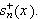 Vi kan dele opp denne ved nullpunktet for
Vi kan dele opp denne ved nullpunktet for

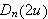 :
:
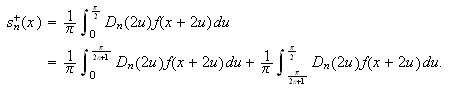
Vi skal vise i Lemma , det såkalte Riemann-Lebesgues Lemma, at det siste
integralet går mot null når

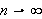 .
Siden
.
Siden

![]() får vi at
får vi at

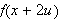 vil ligge rundt
vil ligge rundt

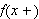 når
når

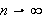 og intervallet
og intervallet

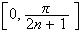 blir mindre og mindre. Men dette burde jo nå tyde på at
blir mindre og mindre. Men dette burde jo nå tyde på at
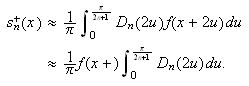
Vi skal snart (via Lemma 19

![]() )
se at arealet under den første slø yfa i
)
se at arealet under den første slø yfa i

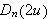 er omtrent
er omtrent

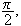 slik at
slik at
![]()
Tilsvarende bemerkning gjelder også for

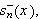 og vi ser da Dirichlets grunn til å prøve å bevise at
og vi ser da Dirichlets grunn til å prøve å bevise at
![]()
Ideen i beviset er at vi må vise at

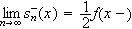 og
og

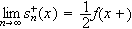 for alle
for alle

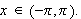 Vi viser da først at vi kan
få
Vi viser da først at vi kan
få
![]()
så nært

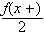 som vi ønsker ved å velge
som vi ønsker ved å velge

![]() tilstrekkelig nær
tilstrekkelig nær

![]() og
og

![]() stor nok, jf. bemerkningene foran. Dernest viser vi at vi kan få resten
av integralet i uttrykket for
stor nok, jf. bemerkningene foran. Dernest viser vi at vi kan få resten
av integralet i uttrykket for

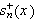 ,
,
![]()
så lite vi vil ved å velge

![]() stor nok. Til det første integralet må vi da ha et intervall
stor nok. Til det første integralet må vi da ha et intervall

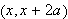 der
der

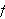 er kontinuerlig. Men selv om (et endelig antall) diskontinuitetspunkter er
tillatt må de separeres av intervaller der
er kontinuerlig. Men selv om (et endelig antall) diskontinuitetspunkter er
tillatt må de separeres av intervaller der

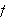 er kontinuerlig. Og her kommer Dirichlets neste antakelse:
er kontinuerlig. Og her kommer Dirichlets neste antakelse:
(iv) Funksjonen

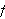 må være
stykkevis kontinuerlig.
Stykevis kontinuerlig medfører integrerbarhet.
%
%comment
må være
stykkevis kontinuerlig.
Stykevis kontinuerlig medfører integrerbarhet.
%
%comment
Dirichlets siste antagelsen er:
(v)

![]() Vi
må ha at
Vi
må ha at

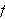 må være
begrenset og stykkevis monoton.
må være
begrenset og stykkevis monoton.
Denne er nok noe mer uklar, og sannsynligvis var det arbeidet med beviset som gjorde at han ble tvunget til å inkludere denne antakelsen. Dirichlet mente at den siste antakelsen ikke var nødvendig, men klarte ikke å beviset teoremet uten å bruke dette. Det var riktig at siste antakelse kan svekkes en del, men først Jordan klarte å utvide teoremet til å gjelde for funksjoner av begrenset variasjon. Som vi ser stilte Dirichlet ganske mange krav til en funksjon for at Fouriers rekkeutviklinger skulle være gyldige!
Vi får også bruk for en versjon av
Riemann-Lebesgues lemma, også kalt
Mercers Note_4 teorem, i beviset for
Dirichlets teorem. Dette lemmaet er en klassiker i Fourierteorien. Riemann
lanserte dette teoremet som en anvendelse av sitt nyinnførte
integralbegrep i verket Über die Darstellbarkeit einer
Funktion durch eine trigonometrische Reihe fra 1854. Lebesgue
videreførte Riemanns resultat i dette lemmaet i 1903. Fra tidligere
å ha sett på Riemann-integrerbare funksjoner ble lemmaet utvidet til
også å holde for Lebesgue-integrerbare funksjoner (til og med
når

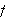 ikke er begrenset).
ikke er begrenset).
[DMB, s.229ff] Hvis

![]() er
her stod det egentlig at funksjonen er kontinuerlig
%comment
monoton
på
er
her stod det egentlig at funksjonen er kontinuerlig
%comment
monoton
på 
 så er
så er
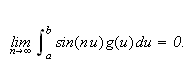
Vi vet at

![]() monoton
på
monoton
på 
![$\left[ a,b\right] $](rekker__273.png) medfører at
medfører at

![]() og dermed
og dermed

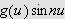 er integrerbar ([TL1, s.326]). Vi må vise at det til
er integrerbar ([TL1, s.326]). Vi må vise at det til

![]() fins et
fins et

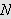 slik at
slik at

![]() medfører
medfører
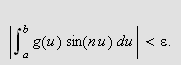
La

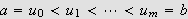 være en partisjon av
være en partisjon av

![$\left[ a,b\right] $](rekker__281.png) slik at hvert intervall har lengde
slik at hvert intervall har lengde

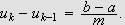 Ideen er nå at vi skal tilnærme
Ideen er nå at vi skal tilnærme

![]() med
med

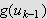 på intervallet
på intervallet

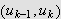 .
Ved dernest å la
.
Ved dernest å la

![]() gå mot uendelig, kan
gå mot uendelig, kan

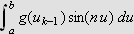 gjøres så lite som ø nskelig. Først deler vi integralet
ved denne partisjonen.
gjøres så lite som ø nskelig. Først deler vi integralet
ved denne partisjonen.
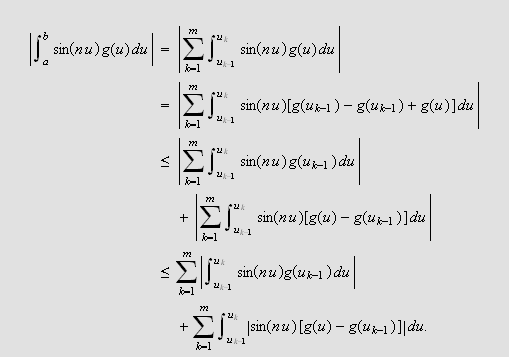
Siden

![]() er monoton på det kompakte intervallet
er monoton på det kompakte intervallet

![]() må den også være begrenset, vi har jo enten
må den også være begrenset, vi har jo enten

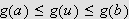 eller
eller

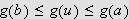 for
for

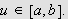 La oss uansett anta
La oss uansett anta

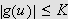 for alle
for alle

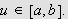 Spesielt er da
Spesielt er da

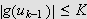 og
og
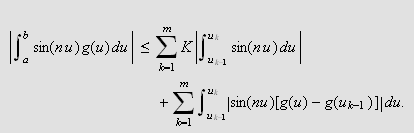
I det første integralet foretar vi en enkel antiderivasjon. Observer for
det andre integralet at

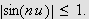 Her er
Her er

![]() monoton og det gir at
monoton og det gir at
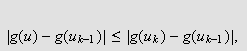
når

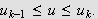 Integralet blir da videre
Integralet blir da videre
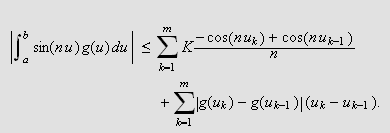
Siden

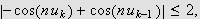 har vi at
har vi at
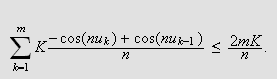
Vi vet også at

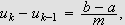 slik at
slik at
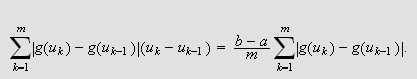
Siden

![]() er monoton på hele
er monoton på hele

![$\left[ a,b\right] $](rekker__308.png) er den enten voksende eller avtakende. Hvis den er voksende, så er
er den enten voksende eller avtakende. Hvis den er voksende, så er
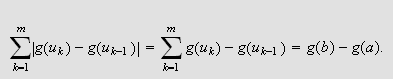
Mens vi hvis

![]() er avtakende har at
er avtakende har at
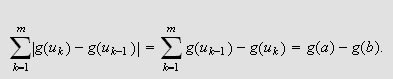
Uansett vil
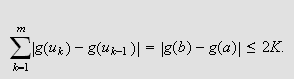
Derfor er
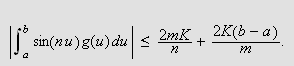
Vi velger
nå 
![]() slik at
slik at

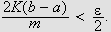 For en slik
For en slik

![]() velges
så
velges
så 
![]() s.a.
s.a.

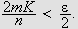 Vi får da
Vi får da
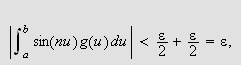
som
ønsket
![]()
Bonnet Note_5 viste i 1849 en alternativ form av mellomverdisetningen. Vi får god bruk for denne varianten og Jordan brukte også denne setningen da han videreførte Dirichlets bevis. Ideen stammer fra såkalt Abelsummasjon, en listig summasjonsmetode gjengitt i følgende teorem:
[DMB, s.168ff] La
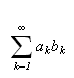
være en rekke der
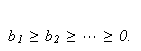
Sett
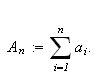
Hvis

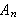 er begrenset, si
er begrenset, si

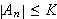 for alle
for alle

![]() så er
så er
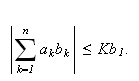
Siden

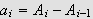 har vi at
har vi at

Siden

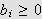 og
og

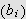 er avtagende har vi at
er avtagende har vi at

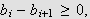 og det gir
og det gir
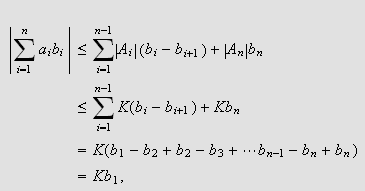
som ønsket.
Vi skal ikke bruke Abels lemma i det følgende, men poengterer at det er ideen med summasjonen som er det essensielle.
Etter mønster av Abels lemma, beviste Bonnet følgende setning:
La

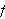 være integrerbar og la
være integrerbar og la

![]() være en ikke-negativ, avtakende funksjon
på
være en ikke-negativ, avtakende funksjon
på 
 Sett
Sett
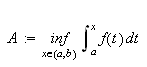
og

Da er
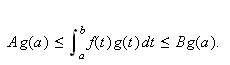
La

![]() være en partisjon av
være en partisjon av

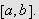 Vi lar
Vi lar
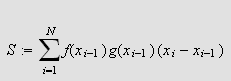
være en tilnærming av
Cauchy-integralet Note_6

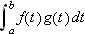 Sett
Sett
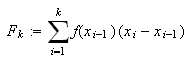
for

![]() og la
og la

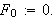 Dette blir på samme måte en tilnærming av Cauchy-integralet
Dette blir på samme måte en tilnærming av Cauchy-integralet

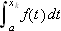 som vi vet oppfyller
som vi vet oppfyller
![]()
for

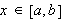 pr. antakelse.
pr. antakelse.
Tilsvarende som i Abels lemma observerer vi nå at
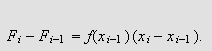
Vi kan bruke samme triks som Abel og skrive

![]() som
som
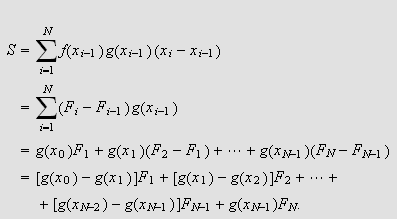
Det er innlysende at

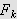 vil avhenge av partisjonen som er brukt. Definer derfor
vil avhenge av partisjonen som er brukt. Definer derfor

![]() og
og

![]() slik at disse vil være øvre og nedre skranke for
slik at disse vil være øvre og nedre skranke for

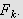 Det vil si
Det vil si

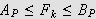 for alle
for alle

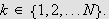 Vi antok at
Vi antok at

![]() er ikke-negativ og avtakende, det vil si at
er ikke-negativ og avtakende, det vil si at

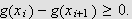 Vi har da
Vi har da
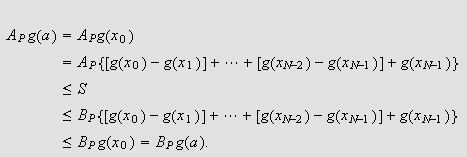
Til gitt

![]() et fins det nå en
et fins det nå en

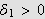 slik at en partisjon med
slik at en partisjon med

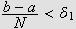 vil gi at
vil gi at
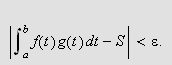
Det fins videre en

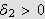 slik at en partisjon med
slik at en partisjon med

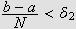 gir
gir
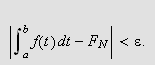
Sett

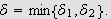
Vi må vise at vi for hver

![]() har
har
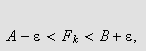
da dette vil gi at
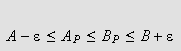
ut fra definisjonen av

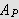 og
og

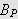 og dermed
og dermed
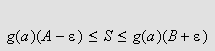
ut fra (). Siden vårt valg av

![]() gir at både () og () holder, må vi også ha at
gir at både () og () holder, må vi også ha at
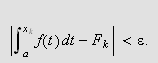
Vi kan nemlig finne en ny partisjon av

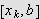 slik at
slik at
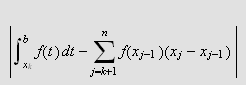
kan bli så lite som ønskelig. Denne finere oppdelingen vil ikke
innvirke
på 
 så vi har fortsatt at
så vi har fortsatt at
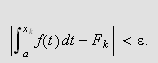
Vi har da at

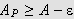 og
og

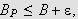 siden
siden

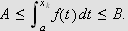 Det følger da at
Det følger da at
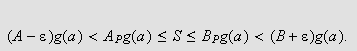
Siden vi har
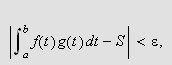
eller sagt på en annen måte,
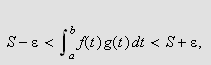
så følger det at
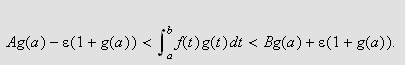
Dette må holde for alle

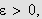 og siden
og siden

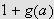 er et fast positivt tall kan vi konkludere med at
er et fast positivt tall kan vi konkludere med at
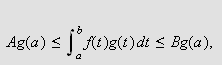
som ønsket.
Resultatet vi trenger i Dirichlets teorem er imidlertid følgende korollar:
La

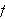 være integrerbar og la
være integrerbar og la

![]() være en ikke-negativ voksende funksjon
på
være en ikke-negativ voksende funksjon
på 
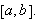 Da fins minst ett tall
Da fins minst ett tall

![]() ,
med
,
med

![]() slik at
slik at
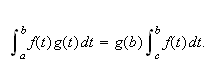
La

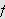 være integrerbar
på
være integrerbar
på 
![$\left[ a,b\right] $](rekker__399.png) og
og

![]() ikke-negativ og voksende
på
ikke-negativ og voksende
på 
![$\left[ a,b\right] $](rekker__401.png) .
Sett
.
Sett

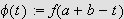 og
og

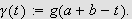 Da vil
Da vil

![]() være ikke-negativ og avtagende, og
være ikke-negativ og avtagende, og

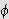 er integrerbar over
er integrerbar over

![$\left[ a,b\right] $](rekker__406.png) .
Disse to funksjonene oppfyller dermed kravene i Teorem . Variabelskiftet
.
Disse to funksjonene oppfyller dermed kravene i Teorem . Variabelskiftet

![]()

![]() gir at
gir at
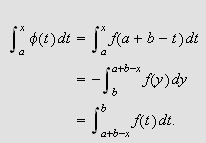
Sett
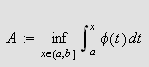
og
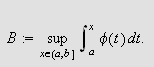
Slik at
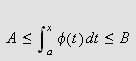
for

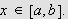 Da er
også
Da er
også
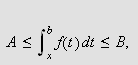
når

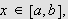 siden
siden

![]() da vil variere fra
da vil variere fra

![]() til
til

![]() Vi vet at
Vi vet at

 og
og

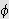 er integrerbare. Siden
er integrerbare. Siden

![]() og
og

![]() er monotone er derfor
også
er monotone er derfor
også 
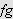 og
og

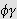 integrerbare ([TL1, s.326]). Det samme variabelskifte som over gir
at
integrerbare ([TL1, s.326]). Det samme variabelskifte som over gir
at
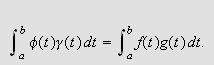
Bonnets middelverdisetning gir da at
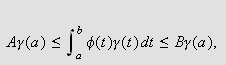
men på grunn av () og definisjonen av

![]() har vi
har vi
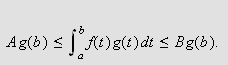
Sett

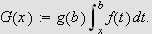 Nå er
Nå er

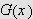 kontinuerlig over
kontinuerlig over

![$\left[ a,b\right] $](rekker__431.png) og den oppnår da sin største og minste verdi,
altså
og den oppnår da sin største og minste verdi,
altså 
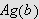 og
og

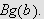 Skjæringssetningen sier da at
Skjæringssetningen sier da at

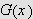 antar enhver verdi mellom
antar enhver verdi mellom

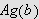 og
og

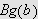 og at det da fins et tall
og at det da fins et tall

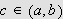 slik at
slik at
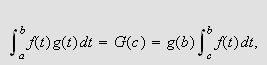
og korollaret er vist.
Til slutt skal vi sammenfatte de ovenstående resultatene og bevise Dirichlets teorem.
[DMB, s.228ff] La

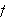 være en begrenset, stykkevis kontinuerlig og stykkevis monoton funksjon
på
være en begrenset, stykkevis kontinuerlig og stykkevis monoton funksjon
på 
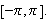 Anta
Anta

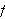 er
er

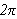 -periodisk
og tilfredsstiller
-periodisk
og tilfredsstiller
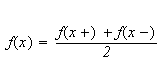
for alle verdier av

![]() La
La

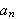 og
og

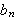 være gitt ved henholdsvis () og (). Da vil for hver verdi av
være gitt ved henholdsvis () og (). Da vil for hver verdi av

![]()
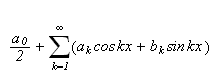
konvergere punktvis mot

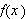 og vi skriver
og vi skriver
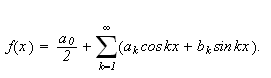
Grensene

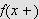 og
og

 vil eksistere siden
vil eksistere siden

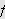 er stykkevis kontinuerlig og begrenset. Som vi har sett, må vi vise at
er stykkevis kontinuerlig og begrenset. Som vi har sett, må vi vise at
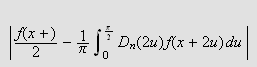
og
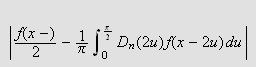
kan gjøres så små vi måtte ønske for tilstrekkelig
store

![]() Vi ser på beviset for den ene påstanden da den andre vil være
helt tilsvarende.
Vi ser på beviset for den ene påstanden da den andre vil være
helt tilsvarende.
La

![]() være gitt. Vi ønsker å vise at det fins et
være gitt. Vi ønsker å vise at det fins et

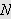 slik at
slik at

![]() medfører
medfører

Punkt (iv) i lemma gir at
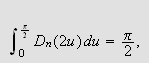
altså at
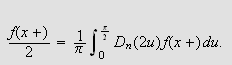
Setter vi inn i () ser vi at vi ønsker å vise at
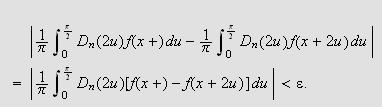
Vi splitter integralet ved punktet

![]() slik:
slik:
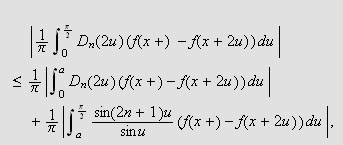
der

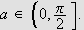 Sett nå
Sett nå
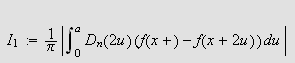
og
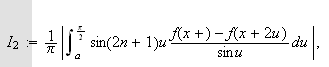
slik at

(i) Vi ser først
på 
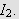 Vi ønsker å bruke Riemann-Lebesgues lemma for å vise at dette
integralet kan gjøres vilkårlig lite. Vi kan ikke bruke lemmaet
direkte (som for øvrig blir gjort i [DMB, s.233]), med
Vi ønsker å bruke Riemann-Lebesgues lemma for å vise at dette
integralet kan gjøres vilkårlig lite. Vi kan ikke bruke lemmaet
direkte (som for øvrig blir gjort i [DMB, s.233]), med

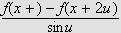 som
som

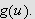 Grunnen til det er at vi ikke har noen garanti for at
Grunnen til det er at vi ikke har noen garanti for at

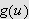 er monoton, som forlangt i lemmaet. Vi vet at
er monoton, som forlangt i lemmaet. Vi vet at

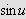 er monotont voksende
på
er monotont voksende
på 
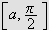 ,
men hvis
,
men hvis

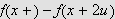 også er monotont voksende kan vi ikke si noe om monotoni-egenskapene til
også er monotont voksende kan vi ikke si noe om monotoni-egenskapene til

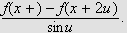 I [DMB, s.228f] står det at
I [DMB, s.228f] står det at
''We shall content ourselves with the theorem as Dirichlet proved it''.
Her er det sannsynligvis et argument som ikke er helt konsistent. Forfatteren
nevner at man egentlig forlanger at

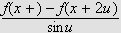 er monoton. Om dette er Dirichlets løsning skal være usagt. Man kom
seg senere unna dette problemet da Jordan innførte begrepet begrenset
variasjon. En annen utvei kunne være å bruke den mer generelle
utgaven av Riemann-Lebesgues Lemma (se kapittel 6) der man ikke stiller krav
til monotonitet. Med
er monoton. Om dette er Dirichlets løsning skal være usagt. Man kom
seg senere unna dette problemet da Jordan innførte begrepet begrenset
variasjon. En annen utvei kunne være å bruke den mer generelle
utgaven av Riemann-Lebesgues Lemma (se kapittel 6) der man ikke stiller krav
til monotonitet. Med

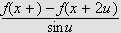 monton gir Riemann-Lebesgues lemma at når
monton gir Riemann-Lebesgues lemma at når

![]() er bestemt, kan vi
få
er bestemt, kan vi
få 
 så lite som ønskelig ved å velge
så lite som ønskelig ved å velge

![]() stor nok. Vi velger derfor først
stor nok. Vi velger derfor først

![]() liten nok til at
liten nok til at

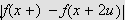 i
i

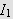 er liten når
er liten når

![]() Dette kan vi gjøre når vi vet
Dette kan vi gjøre når vi vet

![]() er grensen fra høyre for
er grensen fra høyre for

![]()
(ii) Se
så på 
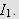 Vi ønsker å gjøre
Vi ønsker å gjøre
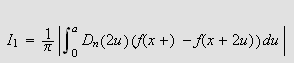
lite, men hvordan vet vi at valget av

![]() ikke avhenger av
ikke avhenger av

![]() ?
Hvis det gjør det, faller argumentet sammen. I det andre integralet vil
valget av
?
Hvis det gjør det, faller argumentet sammen. I det andre integralet vil
valget av

![]() være avhengig av
være avhengig av

![]() og i det første vil
og i det første vil

![]() avhenge av
avhenge av

![]() Og da er vi i samme situasjon som Cauchy befant seg i da han trodde han beviste at alle kombinasjoner av kontinuerlige funksjoner er kontinuerlig. comment
Vi kan i stedet bruke korollaret til Bonnets mellomverdisetning. Vi må ha
at
Og da er vi i samme situasjon som Cauchy befant seg i da han trodde han beviste at alle kombinasjoner av kontinuerlige funksjoner er kontinuerlig. comment
Vi kan i stedet bruke korollaret til Bonnets mellomverdisetning. Vi må ha
at

![]() må være tilstrekkelig nær
må være tilstrekkelig nær

![]() slik at
slik at

![]() er kontinuerlig og monoton
på
er kontinuerlig og monoton
på 
![]() Sett
Sett
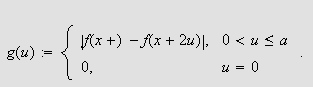
Siden

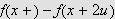 er monoton
på
er monoton
på 
![]() og går mot
og går mot

![]() når
når

![]() går mot
går mot

![]() fra høyre, så er den enten
fra høyre, så er den enten

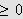 for alle
for alle

![]() eller den er
eller den er

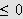 for alle
for alle

![]() Uansett vil
Uansett vil

![]() være positiv og monoton over
være positiv og monoton over

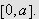 Derfor er
Derfor er
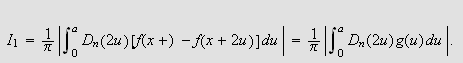
Nå kan vi bruke korollaret til Bonnets mellomverdisetning med

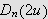 og
og

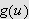 .
Det fins et tall
.
Det fins et tall

![]() mellom
mellom

![]() og
og

![]() s.a.
s.a.

Så skal vi se at for

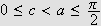 så er
så er
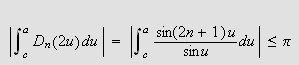
Nullpunktene for

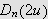 finner vi for
finner vi for

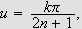 og det første til høyre når
og det første til høyre når

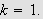 Derivasjon gir
Derivasjon gir
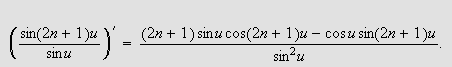
La

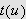 være telleren i (). Derivasjon av denne gir
være telleren i (). Derivasjon av denne gir
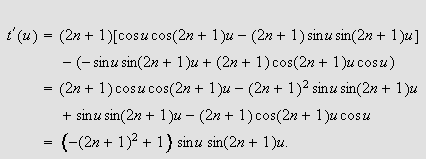
Siden

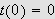 og
og

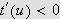 kan vi konkludere med at
kan vi konkludere med at

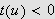 i intervallet
i intervallet

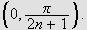 Men det betyr igjen at
Men det betyr igjen at
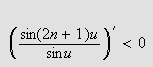
i dette intervallet. Dermed er

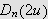 strengt avtakende her. Integranden ser slik ut:
strengt avtakende her. Integranden ser slik ut:
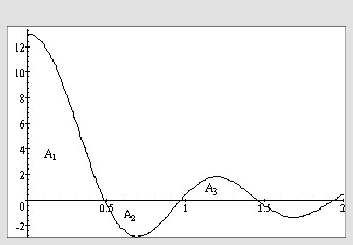
Arealene minker når vi
beveger oss mot høyre
Hvis

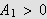 og
og

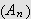 er en alternerende følge som avtar i absoluttverdi så vil
er en alternerende følge som avtar i absoluttverdi så vil

 Det vil si at
Det vil si at
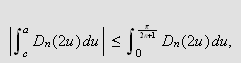
for

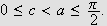 Siden vi har sett at integranden er avtakende mellom
Siden vi har sett at integranden er avtakende mellom

![]() og
og

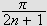 ser vi at første sløyfe ligger inne i rektangelet med bredde
ser vi at første sløyfe ligger inne i rektangelet med bredde

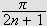 og høyde
og høyde

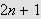 (se lemma
)
(se lemma
)
![]() slik at
slik at
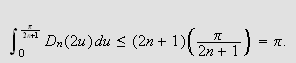
Nå velger vi

![]() tilstrekkelig nær
tilstrekkelig nær

![]() til at
til at

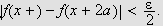 Da følger det at
Da følger det at
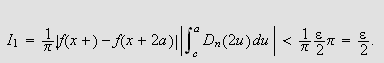
Når

![]() er valgt kan vi velge en
er valgt kan vi velge en

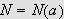 som er slik at
som er slik at

![]() medfører
medfører
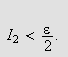
Vi kan da konkludere med at
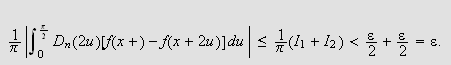
som ønsket i () og alt er bevist.
Kriteriene i Dirichlets teorem kalles ofte Dirichlets kriterier.
Som nevnt mente han at de holdt for en videre klasse funksjoner, eller sagt
på en annen måte, antakelsene i teoremet er unødvendig strenge.
Jordan utvidet senere resultatet om punktvis konvergens av Fourierrekker, og
slo fast at Fourierrekken til en funksjon

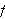 av begrenset variasjon konvergerte punktvis mot
av begrenset variasjon konvergerte punktvis mot

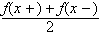 for alle
for alle

![]()
| \lbrack DMB] | Bressoud, D. M.: A radical approach to real analysis |
| The Mathematical Association of America (1993); ISBN: 0883857014 | |
| \lbrack B/N/B] | Bachman, G./Narici, L./Beckenstein, E.: Fourier and Wavelet analysis |
| Springer Verlag New York 2000. ISBN: 0-387-98899-8 | |
| \lbrack JF] | Fourier, J.: Analytical theory of heat |
| Dover publications (1955) | |
| \lbrack D/McK] | Dym, H./McKean, H.P.: Fourier series and integrals |
| Academic press ltd (1972); ISBN: 0-12-226451-7 | |
| \lbrack PRA] | Andenæs, P. R.: MNFMA219 - Reell analyse |
| NTNU (2000) | |
| \lbrack B/B/T] | Bruckner, A.M./Bruckner, J.B./Thomson, B.S.: Real Analysis |
| Prentice Hall int.inc.(1997); ISBN: 0-13-606708-5 | |
| \lbrack KRS] | Stromberg, K.R.: Introduction to classical real analysis |
| Kluwer Academic Publishers (1981); ISBN: 0412742101 |
This document created by Scientific WorkPlace 4.0.