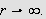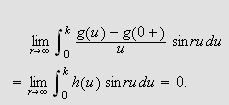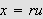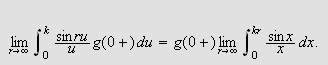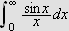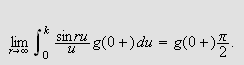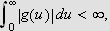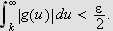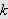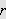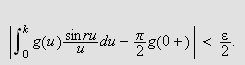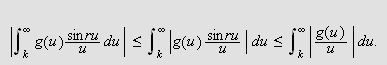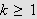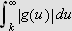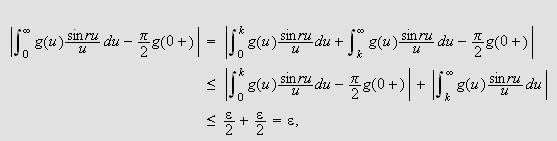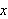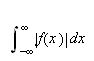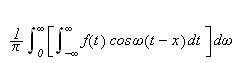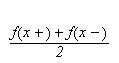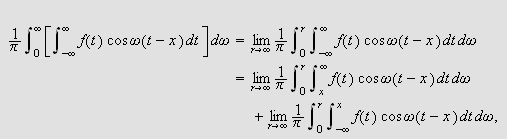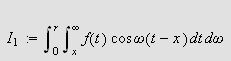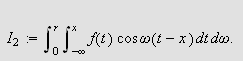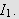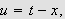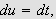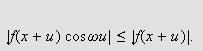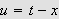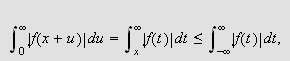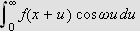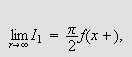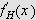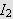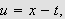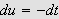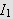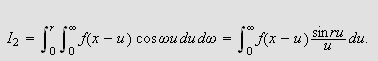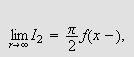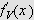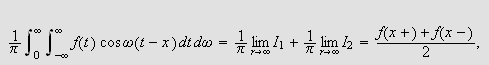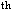FOURIERINTEGRALER
Etter at Fouriers banebrytende ideer hadde sett dagens lys, er det ikke
vanskelig å forstå at det kun dreide seg om tid før disse ble
videre utforsket. Man kan vel også tenke seg flere retninger
utforskningen av Fourieranalysen kunne følge:
-
Finnes det andre måter å konstruere Fourierrekker på, enn ved
å bruke de trigonometriske funksjonene? Hva er så spesielt med sinus
og cosinus at de gjør jobben med å rekonstruere andre funksjoner
så bra? Til og med diskontinuerlige funksjoner kan jo, som vi
så allerede i Fouriers første eksempel, tilnærmes ganske bra,
og vi har via Gibbs fenomen i tillegg B kontroll på feilen som blir
gjort.
-
Hva med flere dimensjoner? Kunne man tenke seg flerdimensjonale Fourierrekker?
Dette kunne jo i såfall være hensiktsmessig dersom man skulle finne
en Fourier-representasjon for flerdimensjonale funksjoner. Eksempel
på dette er fotografier, som kan beskrives via en matrise der
funksjonsverdien i hver celle svarer til fargen i denne cellen.
-
Hva skjedde dersom lederen i varmelikningen var uendelig lang? Der man
før hadde snakket om periodiske funksjoner, kunne man benytte en periode
som var uendelig?
Det første punktet utviklet seg til en helt ny matematisk gren kalt
Wavelets. Det ble sagt (av van Vleck) om denne
teknikken at den ''(...) førte til en helt ny tenkemåte''. Det andre
punktet kan vi også se behandlet flere steder. I [D/McK] finner vi for
eksempel en del om flerdimensjonale Fourierrekker på en standard torus.
Siste punkt tok imidlertid Fourier selv for seg. Vi skal derfor se litt
på dette i denne seksjonen. Vi er nå i den siste delen av Fouriers
bok fra 1822 ([JF]), og dette er altså noe av det han hadde lagt til
etter at hans originale utgave kom ut i 1807.
Trigonometrisk form
Da vi startet i kapittel 1 så vi at Fourier omarbeidet problemet fra
å dreie seg om varmeledning til å omhandle hvilke funksjoner som
kunne representeres ved konvergente trigonometriske rekker. Spesielt
måtte vi finne en Fourierrekke som på en eller annen måte kunne
representere

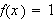 på
på 
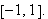 Intuitivt sett skulle man kanskje tro at man kunne erstatte dette intervallet
med hele tallinjen. Et åpenbart problem blir da periodisiteten til de
trigonometriske funksjonene, så helt enkelt er det likevel ikke. Tar man
i betraktning alt som kan skje når man lar noe gå mot uendelig, ser
vi at vi bør være forsiktige. Som regel lever vi i den
misforståelse at våre erfaringer fra den endelige verden kan
overføres til den uendelige. Vi minner her om Cauchys ''bevis'' for at en
uendelig sum av kontinuerlige funksjoner også er kontinuerlig. Vi finner
også følgende motto i [TWK, s.221]:
Intuitivt sett skulle man kanskje tro at man kunne erstatte dette intervallet
med hele tallinjen. Et åpenbart problem blir da periodisiteten til de
trigonometriske funksjonene, så helt enkelt er det likevel ikke. Tar man
i betraktning alt som kan skje når man lar noe gå mot uendelig, ser
vi at vi bør være forsiktige. Som regel lever vi i den
misforståelse at våre erfaringer fra den endelige verden kan
overføres til den uendelige. Vi minner her om Cauchys ''bevis'' for at en
uendelig sum av kontinuerlige funksjoner også er kontinuerlig. Vi finner
også følgende motto i [TWK, s.221]:
''Try to argue about Fourier transforms in the same way as about Fourier
series but do not expect your arguments to hold every time''.
Fouriertransformasjoner er mye brukt i anvendelser. Det er imidlertid ikke
alle bøker som tar for seg bevis for at transformen gjør det den
skal. Dette skyldes kanskje at forfatterne gjerne legger vekt på de mange
anvendelsene for denne teorien. Vi så i kapittel 4 at en
''tilstrekkelig pen'' (i betydningen at den oppfyller
Dirichlet-kriteriene)

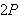 -periodisk
funksjon
-periodisk
funksjon

 generelt kan uttrykkes ved sin Fourierrekke slik:
generelt kan uttrykkes ved sin Fourierrekke slik:
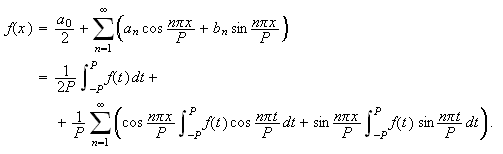
Vi vet nå at denne Fourierrekka konvergerer punktvis mot

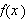 ,
bortsett fra i diskontinuitetspunkter, der rekka konvergerer mot middelverdien
av høyre og venstre grenseverdi ved diskontinuiteten. Hvis vi
nå bruker at
,
bortsett fra i diskontinuitetspunkter, der rekka konvergerer mot middelverdien
av høyre og venstre grenseverdi ved diskontinuiteten. Hvis vi
nå bruker at
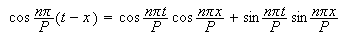
kan vi skrive
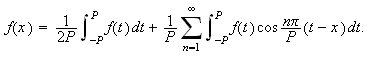
Ideen er at man ved å la

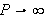 burde kunne få noe som tilsvarer Fourierrekker på et uendelig
intervall. Vi ønsker altså å finne ut hva som skjer med
(f.eks.) temperaturfordeling i en lang leder. Dette er med andre ord en
naturlig videreføring av Fourierrekker. Fourier selv skrev i boken sin
[JF, s. 433]
(
burde kunne få noe som tilsvarer Fourierrekker på et uendelig
intervall. Vi ønsker altså å finne ut hva som skjer med
(f.eks.) temperaturfordeling i en lang leder. Dette er med andre ord en
naturlig videreføring av Fourierrekker. Fourier selv skrev i boken sin
[JF, s. 433]
(
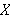 er her integrasjonsområ det):
er her integrasjonsområ det):
''Hvis vi antar

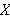 er uendelig, vil leddene i rekka bli differensialer, og summen betegnet ved
er uendelig, vil leddene i rekka bli differensialer, og summen betegnet ved

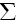 vil bli et bestemt integral (...). Grensene er helt vilkårlige
konstanter''.
vil bli et bestemt integral (...). Grensene er helt vilkårlige
konstanter''.
Vi kan selvfølgelig ikke bare sette

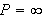 da dette ikke vil gi noen mening. Vi må undersøke grenseprosessen.
Leddet
da dette ikke vil gi noen mening. Vi må undersøke grenseprosessen.
Leddet

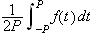 vil gå mot null når
vil gå mot null når

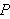 vokser, vel å merke hvis integralet
vokser, vel å merke hvis integralet

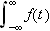

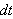 eksisterer og er endelig. Her kommer begrepet integrerbarhet
igjen inn i bildet. Integrerbarhet blir da det første kravet
på
eksisterer og er endelig. Her kommer begrepet integrerbarhet
igjen inn i bildet. Integrerbarhet blir da det første kravet
på 
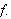
Vi kan erstatte 0 med et hvilket som helst tall i denne definisjonen. For
å illustrere kan vi se på et par enkle eksempler:
Ideen er nå videre at andre ledd på av høyresiden av () minner
om en Riemann-sum med maskevidde

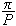 .
For å se dette setter vi
.
For å se dette setter vi

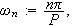 slik at
slik at

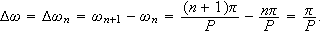 Da får vi
Da får vi
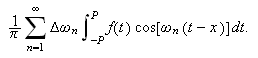
Hvis vi nå setter
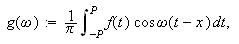
kan andre leddet på høyresiden i () skrives

Når

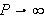 vil
vil

 Dette minner jo da om en Riemann-sum for
Dette minner jo da om en Riemann-sum for

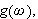 og forhåpentligvis vil () konvergere mot
og forhåpentligvis vil () konvergere mot
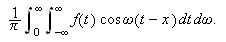
Vi ser at dette integralet ikke trenger å gi mening, men ideen er klar,
vi kan kanskje finne en integralrepresentasjon for

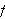 dersom funksjonen er ''pen'' nok.
dersom funksjonen er ''pen'' nok.
Vi ser tydelig analogien til vanlige Fourierrekker; en kontinuerlig variabel

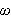 i stedet for indeksen vi hadde tidligere,
i stedet for indeksen vi hadde tidligere,

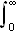 i stedet for
i stedet for

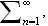 og
og

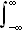 i stedet for
i stedet for

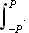 Forhåpentligvis kan vi vise at Fourierintegralet for
Forhåpentligvis kan vi vise at Fourierintegralet for

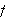 konvergerer mot
konvergerer mot

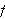 for alle
for alle

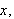 eller for visse
eller for visse

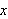 hvis vi legger restriksjoner
på
hvis vi legger restriksjoner
på 
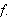
På samme måte som vi har en kompleks versjon av Fourierrekkene har
vi det også for integralformelen, bedre kjent som Fouriertransformasjon.
Dette er et veldig nyttig verktøy i anvendt matematikk, og er
så godt som uunværlig i fysikk og informatikk. Vi skal holde oss til
Fouriers trigonometri-versjon, og nevner bare litt om den eksponensielle
formen her.
Eksponensiell form
Denne kan oppnås på samme måte, vi skriver opp den generelle
Fourierrekka, og lar perioden gå mot uendelig. Vi minner her om at vi
generelt har den komplekse Fourierkoeffisienten gitt ved
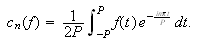
Hvis funksjonen er tilstrekkelig pen vil Fourierrekka til

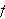
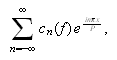
konvergere punktvis mot

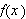 der denne er kontinuerlig. Vi har videre
der denne er kontinuerlig. Vi har videre
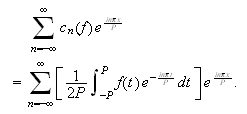
Igjen setter vi

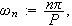 slik at
slik at

 Vi får da at denne summen kan skrives
Vi får da at denne summen kan skrives
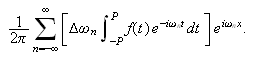
Setter vi

ender vi opp med
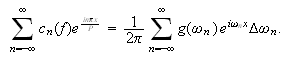
Igjen likner dette på en Riemann-sum. Lar vi

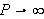 kan det se ut som om vi har:
kan det se ut som om vi har:
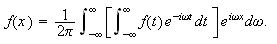
Det kan, dersom dette siste integralet eksisterer, vises at den inverse
Fouriertransformen rekonstruerer

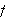 slik at
slik at
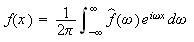
for alle

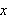 under bestemte betingelse
på
under bestemte betingelse
på 
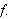 Faktoren
Faktoren

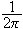 står noen steder i transformasjonsformelen og andre ganger i den inverse
transformasjonsformelen. I noen bøker finner vi også at det
står
står noen steder i transformasjonsformelen og andre ganger i den inverse
transformasjonsformelen. I noen bøker finner vi også at det
står

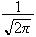 i begge formlene, sannsynligvis for å framstille formelsettet mer
symmetrisk. Andre notasjoner for Fouriertransformen er
i begge formlene, sannsynligvis for å framstille formelsettet mer
symmetrisk. Andre notasjoner for Fouriertransformen er

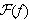 eller
eller

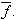 Vi merker oss også likheten mellom Fouriertransformen og komplekse
Fourierkoeffisienter. Vi kunne skrevet
Vi merker oss også likheten mellom Fouriertransformen og komplekse
Fourierkoeffisienter. Vi kunne skrevet
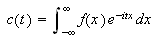
og
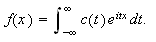
Her transformerer vi først

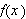 og får
og får

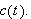 Så bruker vi den inverse transformeren for å få tilbake
Så bruker vi den inverse transformeren for å få tilbake

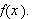 På samme måte finner vi Fourierkoeffisienter for
så å summere Fourierrekken for å rekonstruere
På samme måte finner vi Fourierkoeffisienter for
så å summere Fourierrekken for å rekonstruere

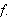
Det er for øvrig på grunn av nytteverdien i sammenhenger med
elektronikk og e-lære at mange foretrekker å benytte

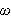 som variabel (symboliserer frekvens) i stedet for den tidligere mer vanlige
som variabel (symboliserer frekvens) i stedet for den tidligere mer vanlige

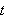 (symboliserer tid). Det er også en hel mengde andre anvendelser av
Fouriertransformen. Det fins for eksempel en sammennheng mellom posisjonen og
impulsen til en partikkel via denne transformen. Man har kanskje hørt om
Heisenbergs usikkerhetsprinsipp, som slår fast at
vi bare kan kjenne til en av størrelsene fart og posisjon nøyaktig
på samme tid (se f.eks. [D/McK]). I tillegg brukes jo både
Fourierrekker og Fouriertransformen for å løse diff.likninger.
(symboliserer tid). Det er også en hel mengde andre anvendelser av
Fouriertransformen. Det fins for eksempel en sammennheng mellom posisjonen og
impulsen til en partikkel via denne transformen. Man har kanskje hørt om
Heisenbergs usikkerhetsprinsipp, som slår fast at
vi bare kan kjenne til en av størrelsene fart og posisjon nøyaktig
på samme tid (se f.eks. [D/McK]). I tillegg brukes jo både
Fourierrekker og Fouriertransformen for å løse diff.likninger.
Følger vi for eksempel framstillingen i [B/C] ser vi at veien til et
bevis for at en integralrepresentasjon er gyldig er veldig lik den for
Fourierrekker, dog litt mer avansert. Det er altså en analogi, selv om
denne ikke kan følges helt.
Vi skal igjen innom Riemann-Lebesgues lemma. Vi tar nå skrittet fra
å la grensen gå over

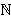 ,
til å gå kontinuerlig over
,
til å gå kontinuerlig over

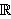 .
Her skal vi bruke uniformt kontinuitet, noe Dirichlet ikke kjente til da han
publiserte sitt bevis for punktvis konvergens av Fourierrekker.
.
Her skal vi bruke uniformt kontinuitet, noe Dirichlet ikke kjente til da han
publiserte sitt bevis for punktvis konvergens av Fourierrekker.
Så trenger vi Dirichlets integral, som spiller
tilsvarende rolle som Dirichlet-kjernen i forrige kapittel. Verdien var kjent
også for Fourier, og han skrev selv:
''Undersøk først det bestemte integralet

 som vi vet er lik
som vi vet er lik

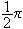 [JF, s. 426].''
[JF, s. 426].''
og tidligere (om det samme integralet)
''Denne verdien har vært kjent en tid [JF, s. 346].''
La oss først beregne dette integralet. Vi får da bruk for
følgende begrep:
Lemma (Dirichlets
integral)
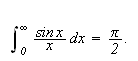
Fouriers integralteorem
Litteratur
| \lbrack TWK] |
Körner: Fourier analysis |
|
Cambridge university press (1988); 0-521-25120-6 |
| \lbrack D/McK] |
Dym, McKean: Fourier series and integrals |
|
Academic press ltd (1972); ISBN: 0-12-226451-7 |
| \lbrack B/C] |
Brown, Churchill: Fourier series and boundary value
problems, 6
  ed.
ed. |
|
McGraw-Hill Higher education (2001); ISBN: 0071181512 |
| \lbrack JM] |
Mason: Thinking mathematically |
|
Addison Wesley Publishing Company (1982); ISBN: 0201102382 |
| \lbrack PRA] |
Andenæs: MNFMA219 Reell analyse |
|
NTNU |
| \lbrack TL1] |
Lindstrøm: Kalkulus |
|
Universitetsforlaget AS (1995); ISBN: 82-00-22472-4 |
| \lbrack JF] |
Fourier: The analytical theory of heat |
|
Dover publications (1955) |
| \lbrack TG] |
Gulliksen: Matematikk i praksis |
|
Universitetsforlaget AS (1996); ISBN: 82-00-22548-8 |
This document created by Scientific WorkPlace 4.0.
Neste: Parallell til skolen
Forrige: Fejerkjernen

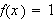 på
på 
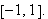 Intuitivt sett skulle man kanskje tro at man kunne erstatte dette intervallet
med hele tallinjen. Et åpenbart problem blir da periodisiteten til de
trigonometriske funksjonene, så helt enkelt er det likevel ikke. Tar man
i betraktning alt som kan skje når man lar noe gå mot uendelig, ser
vi at vi bør være forsiktige. Som regel lever vi i den
misforståelse at våre erfaringer fra den endelige verden kan
overføres til den uendelige. Vi minner her om Cauchys ''bevis'' for at en
uendelig sum av kontinuerlige funksjoner også er kontinuerlig. Vi finner
også følgende motto i [TWK, s.221]:
Intuitivt sett skulle man kanskje tro at man kunne erstatte dette intervallet
med hele tallinjen. Et åpenbart problem blir da periodisiteten til de
trigonometriske funksjonene, så helt enkelt er det likevel ikke. Tar man
i betraktning alt som kan skje når man lar noe gå mot uendelig, ser
vi at vi bør være forsiktige. Som regel lever vi i den
misforståelse at våre erfaringer fra den endelige verden kan
overføres til den uendelige. Vi minner her om Cauchys ''bevis'' for at en
uendelig sum av kontinuerlige funksjoner også er kontinuerlig. Vi finner
også følgende motto i [TWK, s.221]:
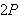
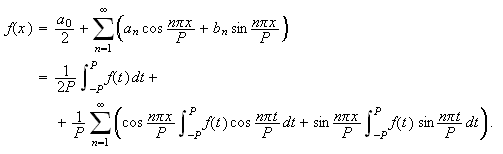
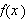
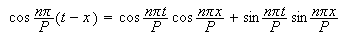
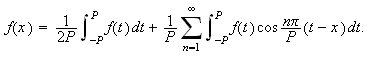
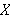
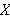
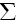
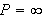
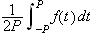
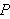
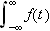
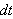
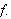
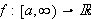
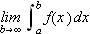
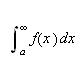
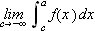
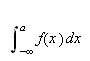
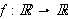
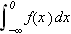
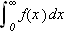
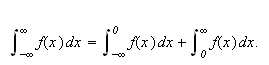
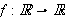
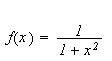
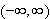
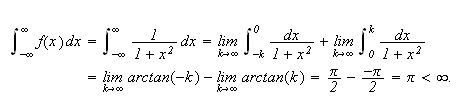
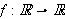
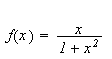
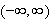
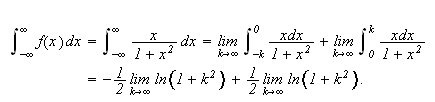
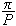
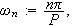
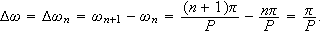
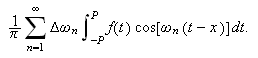
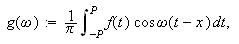

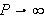

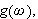
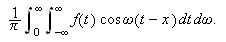
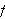
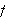
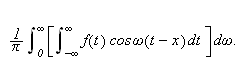
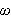
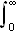
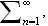
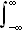
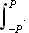
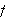
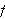
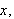
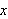
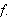
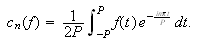
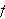
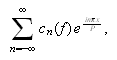
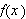
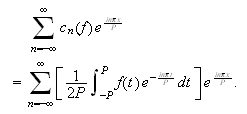
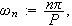

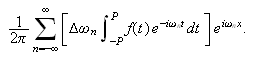

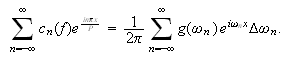
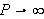
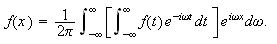
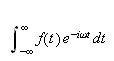

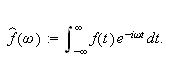
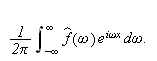
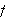
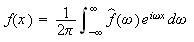
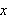
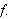
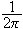
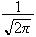
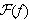
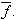
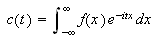
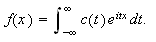
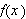
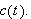
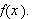
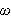
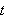
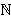
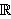
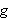
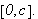
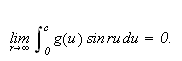
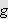
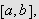
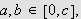
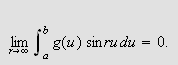
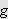
![$\left[ a,b\right] $](trans__102.png)
![$\left[ a,b\right] $](trans__103.png)

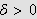
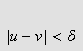
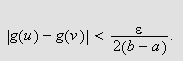
![$\left[ a,b\right] $](trans__108.png)
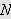
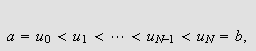
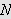
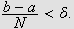
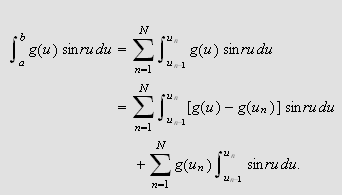
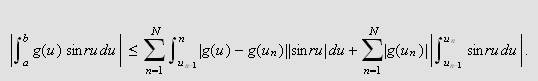
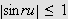
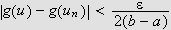
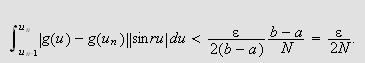

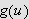
![$\left[ a,b\right] $](trans__120.png)
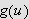
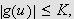
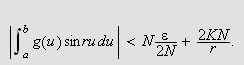
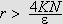
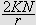
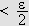
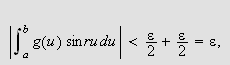

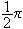
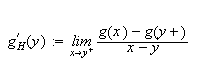
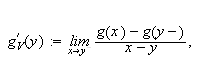
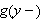
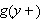
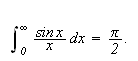
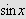
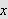
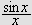
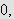
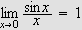
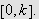
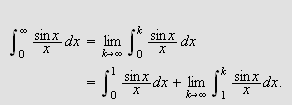
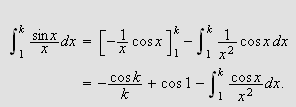

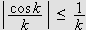
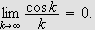
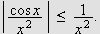
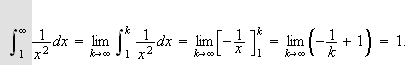
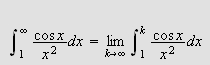
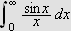

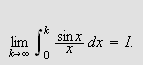
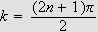
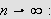
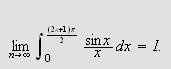
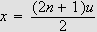
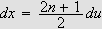
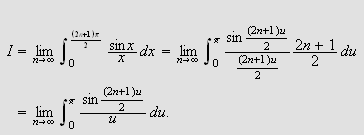
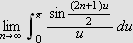
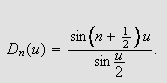
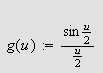
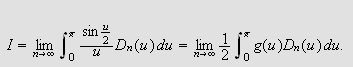
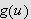
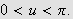
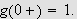
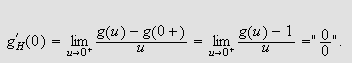

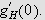
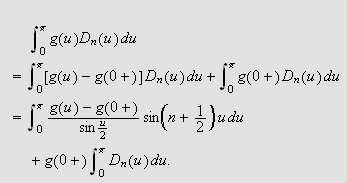
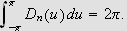
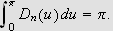
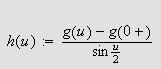
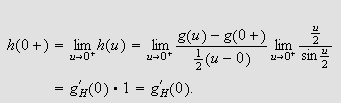
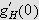
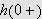
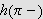
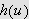
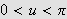
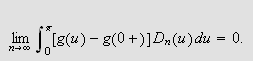
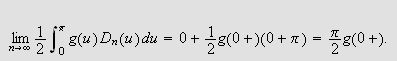
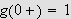
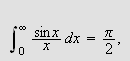
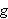
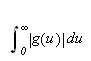
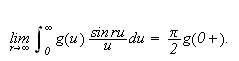
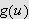
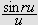
![$\left[ a,b\right] $](trans__189.png)
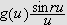
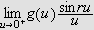

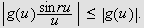
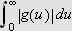
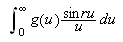
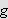
![$\left[ 0,k\right] $](trans__199.png)
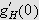
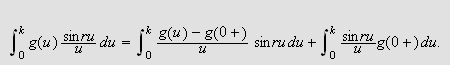
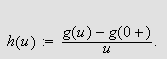
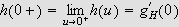
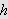
![$\left[ 0,k\right] $](trans__205.png)