

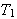 og
og

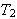 er separerte i en avstand
er separerte i en avstand



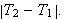 Videre er varmestrømmen omvendt proporsjonal med avstanden
Videre er varmestrømmen omvendt proporsjonal med avstanden

''Varme gjennomtrenger, på samme måte som tyngdekraft, alle stoff i universet. Varmestrålene fins i alle deler av rommet. Vi skal i dette arbeidet stille opp de matematiske lovene varme følger. Varmeteorien vil heretter danne en av de viktigste grenene i generell fysikk.'' (Joseph Fourier - The analytical theory of heat [JF, s. 1])
Vi skal i dette kapittelet se på bruk av Fourierreker i partielle differensiallikninger. Eksempler er varmeledning og bølgeforplantning. Fourier selv var altså opptatt av varmeledning, og var mer interessert i å forstå fysikken for å stille opp problemet enn matematikken for å løse det. Det passer derfor bra å gi en utledning av varmelikningen her. En slik utledning er standard og vi finner den i de fleste bøker der andre ordens diff.likninger er behandlet. Eksempel på slik litteratur er den mye brukte [B/DiP].
Ved å finne to ekvivalente uttrykk for varmestrømmen i en tynn leder kan vi sette disse like hverandre og dermed oppnå en likning som beskriver temperaturen i lederen.
Et kjent fysisk prinsipp er at varmemengden som strømmer gjennom en del av en leder på et bestemt sted pr. tidsenhet er proporsjonal med gradienten til temperaturen. Dette prinsippet bygger igjen på Newtons avkjølingslov:
''Hvis to parallelle plater med samme areal

![]() og forskjellige temperaturer
og forskjellige temperaturer

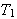 og
og

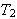 er separerte i en avstand
er separerte i en avstand

![]() vil det strømme en varmemengde fra den varmeste plata til den kaldeste
(vi må alltid ha et varmt sted og et kaldt sted skal varme ledes).
Varmemengden som ledes pr. tidsenhet er proporsjonal med denne flaten
vil det strømme en varmemengde fra den varmeste plata til den kaldeste
(vi må alltid ha et varmt sted og et kaldt sted skal varme ledes).
Varmemengden som ledes pr. tidsenhet er proporsjonal med denne flaten

![]() og temperaturforskjellen mellom platene,
og temperaturforskjellen mellom platene,

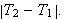 Videre er varmestrømmen omvendt proporsjonal med avstanden
Videre er varmestrømmen omvendt proporsjonal med avstanden

![]() mellom platene.''
mellom platene.''
Vi har
altså
![]()
der

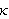 (kappa) er en proporsjonalitetskonstant kalt termisk
konduktivitet (eng.: conduct = lede). Det er også naturlig at
denne avhenger av hvilket materiale som befinner seg mellom platene. Den gir
derfor et mål på hvor bra eller dårlig et stoff leder varme.
Dette er en empirisk lov, og Fourier fant også fram til dette resultatet
([JF, s.42]).
(kappa) er en proporsjonalitetskonstant kalt termisk
konduktivitet (eng.: conduct = lede). Det er også naturlig at
denne avhenger av hvilket materiale som befinner seg mellom platene. Den gir
derfor et mål på hvor bra eller dårlig et stoff leder varme.
Dette er en empirisk lov, og Fourier fant også fram til dette resultatet
([JF, s.42]).
La oss nå legge en tynn, sylindrisk varmeleder fra

![]() til
til

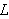 langs
langs

![]() -aksen.
Vi antar lederen er laget av et homogent materiale og har likt tverrsnitt over
det hele. Denne lederen må være isolert slik at det ikke
strømmer varme gjennom sidene, men kun langs lederen og ut og inn gjennom
endene. Vi antar også at temperaturfunksjonen
-aksen.
Vi antar lederen er laget av et homogent materiale og har likt tverrsnitt over
det hele. Denne lederen må være isolert slik at det ikke
strømmer varme gjennom sidene, men kun langs lederen og ut og inn gjennom
endene. Vi antar også at temperaturfunksjonen

![]() og de deriverte
og de deriverte

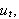

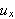 og
og

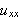 er kontinuerlige og kun avhenger av posisjonen
er kontinuerlige og kun avhenger av posisjonen

![]() i lederen og tiden
i lederen og tiden

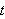 (altså har ikke
(altså har ikke

![]() og
og

![]() noen betydning - temperaturen er konstant over et tverrsnitt av lederen).
Dette er en bra tilnærmelse når lederen er veldig tynn.
noen betydning - temperaturen er konstant over et tverrsnitt av lederen).
Dette er en bra tilnærmelse når lederen er veldig tynn.
Vi ser på delen av lederen mellom

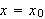 og
og

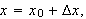 se på figuren.
se på figuren.
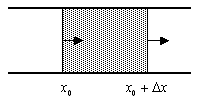
Et segment av lederen
Varmemengden som nå strømmer inn i segmentet
(skravert område på figuren) pr. tidsenhet minus varmemengden som
strømmer ut av segmentet pr. tidsenhet må være lik den netto
varmeøkning pr. tidsenhet i dette segmentet. Newtons avkjø lingslov
gir at varmemengden som nå strømmer gjennom lederen fra

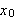 til
til

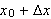 pr. tidsenhet er
pr. tidsenhet er
![]()
Varmestrømmen gjennom tverrsnittet ved

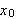 kaller vi
kaller vi

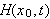 .
Denne er definert ved
.
Denne er definert ved
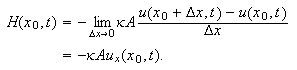
Minustegnet skyldes at det vil være en positiv varmeflyt fra venstre mot
høyre hvis temperaturen er mindre i

 enn i
enn i

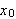 .
En annen måte å si dette på er at varme strømmer fra et
varmt sted til et kaldt sted, og varmeflyten er da positiv selv om den
deriverte av temperaturen,
.
En annen måte å si dette på er at varme strømmer fra et
varmt sted til et kaldt sted, og varmeflyten er da positiv selv om den
deriverte av temperaturen,

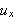 ,
er negativ. Ved posisjonen
,
er negativ. Ved posisjonen

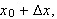 vil varmestrømmen (altså varmemengde pr. tid) på samme
måte være
vil varmestrømmen (altså varmemengde pr. tid) på samme
måte være
![]()
Totalt er endringen pr. tidsenhet i varmemengden i delen av lederen mellom

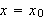 og
og

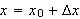
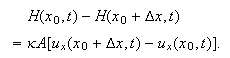
Siden

 er kontinuerlig kan vi bruke fundamentalteoremet (se
f.eks. [TL1, s. 335]) som gir
er kontinuerlig kan vi bruke fundamentalteoremet (se
f.eks. [TL1, s. 335]) som gir
![]()
Nå skal vi utlede et annet uttrykk for total varmeendring pr. tidsenhet.
Temperaturen i segmentet avhenger også av
tettheten

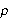 (g/cm
(g/cm
 til materialet og den spesifikke varmekapasiteten
til materialet og den spesifikke varmekapasiteten

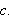 Spesifikk varmekapasitet er den varmemengde som trengs for å øke
temperaturen i ett gram av et bestemt materiale en grad. Det vil si at
Spesifikk varmekapasitet er den varmemengde som trengs for å øke
temperaturen i ett gram av et bestemt materiale en grad. Det vil si at

![]() er den mengden som trengs for å øke temperaturen i
er den mengden som trengs for å øke temperaturen i

![]() cm
cm
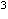 av materialet fra
av materialet fra

![]() grader til
grader til

![]() grader. I segmentet på figuren trengs da en varme
på
grader. I segmentet på figuren trengs da en varme
på
![]()
for å øke temperaturen fra

![]() til
til

![]() Derivasjon under integraltegnet er tillatt, siden både
Derivasjon under integraltegnet er tillatt, siden både

![]() og
og

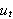 er antatt kontinuerlige (se f.eks. [PRA, s. 37]). Varmeendring pr. tidsenhet i
segmentet er derfor
er antatt kontinuerlige (se f.eks. [PRA, s. 37]). Varmeendring pr. tidsenhet i
segmentet er derfor
![]()
Vi har nå to uttrykk for varmeendringen pr. tidsenhet i segmentet, i
() og (). Disse må være like, og vi får da
![]()
eller
![]()
Dette må holde for alle valg av

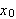 og
og

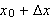 Siden
Siden

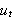 og
og

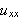 er kontinuerlige vil integranden være kontinuerlig. Dermed
må integranden være eksakt lik null,
er kontinuerlige vil integranden være kontinuerlig. Dermed
må integranden være eksakt lik null,
![]()
eller
![]()
Sett

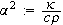 (for å gjøre senere utregninger enklere). Vi ender da opp med
(for å gjøre senere utregninger enklere). Vi ender da opp med
![]()
Dette er altså den endimensjonale varmelikningen.
Verdier for konstanten

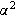 kan finnes i tabeller.
kan finnes i tabeller.
La oss nå gi en fullstendig løsning av varmelikningen i følgende situasjon:
Temperaturen i

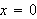 og
og

![]() er lik null, og utgangspunktet for temperaturfordelingen er en kjent funksjon
er lik null, og utgangspunktet for temperaturfordelingen er en kjent funksjon

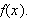 Problemet er altså
Problemet er altså
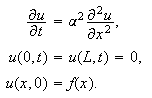
Vi går fram på tilsvarende måte som Fourier gjorde da han
løste varmelikningen for en semi-uendelig plate. Metoden er standard i
dag, og det påstås altså i noe litteratur at Fourier var den
første som brukte separasjon av variable til å løse slike
likninger.
Vi antar løsningen har formen

![]() Vi skal senere se at denne antagelsen kan rettferdiggjøres. Innsatt i ()
får vi at
Vi skal senere se at denne antagelsen kan rettferdiggjøres. Innsatt i ()
får vi at
![]()
Separasjon av variablene
gir
![]()
Siden venstresiden kun er avhengig av

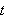 og høyresiden kun av
og høyresiden kun av

![]() må begge være lik en konstant som vi kaller
må begge være lik en konstant som vi kaller

 Minustegnet skyldes at uttrykkene vi senere kommer fram til blir enklere. Vi
ender da opp med de to likningene
Minustegnet skyldes at uttrykkene vi senere kommer fram til blir enklere. Vi
ender da opp med de to likningene
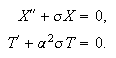
Nå setter vi inn randbetingelsene

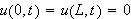 ,
slik at vi må ha
,
slik at vi må ha
![]()
For at dette skal stemme kan vi ha

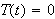 for alle
for alle

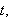 men da vil jo
også
men da vil jo
også 
![]() for alle
for alle

![]() og
og

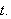 Det betyr igjen at betingelsen
Det betyr igjen at betingelsen

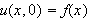 ikke kan oppfylles for andre
ikke kan oppfylles for andre

 enn
enn

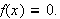 Derfor ser vi oss nødt til å ha
Derfor ser vi oss nødt til å ha

![]() På samme måte må vi ha
På samme måte må vi ha

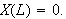
Vi ser så på tre muligheter for valg av

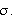
Først lar vi

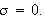 Da får vi fra () at
Da får vi fra () at

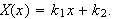 Vi må velge
Vi må velge

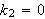 og
og

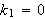 for å tilfredsstille randbetingelsene
for å tilfredsstille randbetingelsene

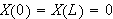 ,
og vi finner ingen ikke-trivielle løsninger for dette valg av
,
og vi finner ingen ikke-trivielle løsninger for dette valg av

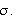
Ser
så på 
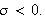 Settes
Settes

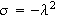 får vi likningen
får vi likningen

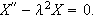 Løsningen av denne er
Løsningen av denne er
![]()
(Man vil enkelte steder finne denne løsningen utskrevet ved hyperbolske
funksjoner, dette er en smakssak.) Randbetingelsene gir igjen

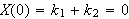 og
og

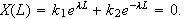 Fra
Fra

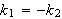 får vi
får vi

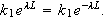 Men dette stemmer jo bare når
Men dette stemmer jo bare når

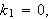 og vi må derfor også ha
og vi må derfor også ha

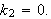 Også her vil vi da ende opp med den trivielle løsningen.
Også her vil vi da ende opp med den trivielle løsningen.
Siste mulighet for å finne ikke-trivielle løsninger er

 Sett da
Sett da

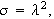 slik at vi får likningen
slik at vi får likningen

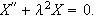 Løsningen av denne er
Løsningen av denne er
![]()
Initialbetingelsene gir nå at

![]() og
og

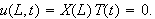 Siden
Siden

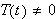 følger det at
følger det at

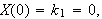 og videre
at
og videre
at 
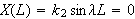 med
med

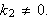 For å få ikke-trivielle løsninger
må
For å få ikke-trivielle løsninger
må 
![]() .
Sett
.
Sett

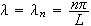 der
der

![]() Setter vi
Setter vi

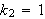 får vi løsningen
får vi løsningen
![]()
Vi trenger ikke ta med negative

![]() siden
siden

 og dette fortegnsskiftet kan fanges opp av en konstant foran sinusleddet.
Funksjonen
og dette fortegnsskiftet kan fanges opp av en konstant foran sinusleddet.
Funksjonen

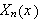 tilfredsstiller randbetingelsene og diff.likningen ().
tilfredsstiller randbetingelsene og diff.likningen ().
Vi ser så på (). Generell løsning av denne er
![]()
der

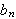 er en
proporsjonalitetskonstant
er en
proporsjonalitetskonstant
![]() Vi ser da at funksjonen
Vi ser da at funksjonen
![]()
vil tilfredsstille varmelikningen og randbetingelsene.
Fremdeles gjenstår å tilfredsstille initialbetingelsen

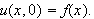 La oss se på en endelig sum av slike løsninger som (),
La oss se på en endelig sum av slike løsninger som (),
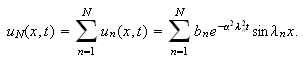
Vi vet at også denne summen vil være en løsning av
varmelikningen (varmelikningen er lineær) og samtidig oppfylle
randbetingelsene

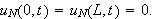 Setter vi
Setter vi

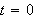 ,
som i betingelsen, får vi
,
som i betingelsen, får vi
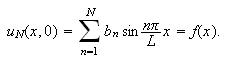
Nå er problemet å forsøke å justere konstantene

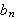 slik at denne likheten holder. Men hvis ikke
slik at denne likheten holder. Men hvis ikke

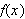 har formen
har formen
![]()
så fins ikke

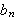 som oppfyller likheten [B/DiP, s. 517]. Dette gir en indikasjon på at vi
kan prøve å finne en løsning bestående av en uendelig sum,
nemlig
som oppfyller likheten [B/DiP, s. 517]. Dette gir en indikasjon på at vi
kan prøve å finne en løsning bestående av en uendelig sum,
nemlig

Vi har
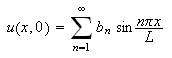
og dette skal være lik

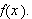 Dermed innser vi at
Dermed innser vi at

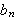 må være nettopp Fourierkoeffisientene i sinusrekken til
må være nettopp Fourierkoeffisientene i sinusrekken til

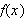 .
Vi har allerede sett hvordan Fourier regnet ut koeffisientene
.
Vi har allerede sett hvordan Fourier regnet ut koeffisientene

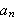 for å representere en funksjon ved en cosinus-rekke på et gitt
intervall. Ø nsker vi en sinusrekke får vi en tilsvarende formel,
der
for å representere en funksjon ved en cosinus-rekke på et gitt
intervall. Ø nsker vi en sinusrekke får vi en tilsvarende formel,
der
![]()
Utregningen er lik den vi så i forrige kapittel. Det kan kanskje virker
rart at man noen steder bruker bare cosinus-ledd for å representere
funksjoner, og andre steder bare sinus-ledd. I tillegg brukes generelt begge
deler samtidig! Poenget her er at en gitt funksjon kan forlenges
på bå de en like og en odde måte, slik at man kan velge om man
vil bruke en cosinus-, sinus- eller kombinert representasjon.
Den totale løsningen på varmelikningen er da:
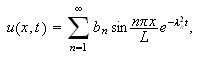
der

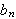 er gitt ved ().
er gitt ved ().
For å kommentere den fysiske meningen med løsningen, kan vi merke
oss at ledd av typen
![]()
inngår i løsningen, slik at en høyere konduktivitet i
materialet vil gi en større

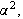 og temperaturen i en slik stang vil dermed gå raskere mot null når
vi tiden går.
og temperaturen i en slik stang vil dermed gå raskere mot null når
vi tiden går.
Er man kritisk vil man kanskje stille seg spørrende til hvorledes man kan
unnlate å se på muligheten for at varmelikningen () har
løsninger av andre typer enn

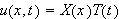 .
Generelt vil jo gjerne en funksjon
.
Generelt vil jo gjerne en funksjon

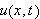 ikke kunne skrives som et produkt
ikke kunne skrives som et produkt

 Hvis vi nå hadde hatt en alternativ løsning av varmelikningen,
så ville vi jo ikke kunne forutsi temperaturen på et gitt sted til
en bestemt tid ved hjelp av løsningen vi har funnet. Derfor ønsker
vi at løsningen vi har funnet skal være den eneste rette.
Hvis vi nå hadde hatt en alternativ løsning av varmelikningen,
så ville vi jo ikke kunne forutsi temperaturen på et gitt sted til
en bestemt tid ved hjelp av løsningen vi har funnet. Derfor ønsker
vi at løsningen vi har funnet skal være den eneste rette.
La
nå 
![]() være kontinuerlig på det semi-uendelige rektangelet
være kontinuerlig på det semi-uendelige rektangelet

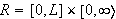 i
i

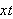 -planet.
Anta også at
-planet.
Anta også at

![]() er en løsning av varmelikningen () for
er en løsning av varmelikningen () for

![]() og
og

![]() For en gitt
For en gitt

![]() definerer vi rektangelet
definerer vi rektangelet

 og la
og la

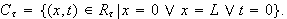
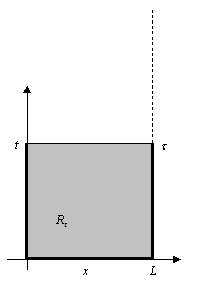
Rektangelet

 og randen
og randen

Her er

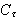 altså den kraftige streken. Vi minner om at vi fremdeles ser på den
endimensjonale varmelikningen selv om vi illustrerer problemet i et plan. Vi
starter med et resultat vi får bruk for.
altså den kraftige streken. Vi minner om at vi fremdeles ser på den
endimensjonale varmelikningen selv om vi illustrerer problemet i et plan. Vi
starter med et resultat vi får bruk for.
Hvis løsningen

![]() av varmelikningen er kontinuerlig
på
av varmelikningen er kontinuerlig
på 
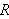 og
og

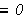 på
på 
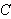 (randen til
(randen til

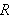 )
så er
)
så er

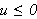 i hele
i hele

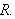
Vi ønsker en selvmotsigelse og antar det motsatte, nemlig at det fins et
punkt

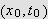 i det indre av
i det indre av

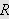 slik at
slik at

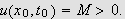 Velg
så
Velg
så 
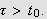 Da vil
Da vil

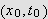 ligge inne i rektanglet
ligge inne i rektanglet

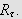 Definer hjelpefunksjonen
Definer hjelpefunksjonen
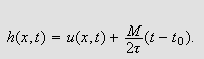
for

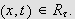 Vi ser
så på
Vi ser
så på 
![]() på
på 
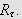 Nå er
Nå er

![]() kontinuerlig
på
kontinuerlig
på 
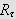 og
og

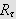 er
kompakt
er
kompakt
![]() Da vet vi (se f.eks. [PRA, s. 29]) at
Da vet vi (se f.eks. [PRA, s. 29]) at

![]() oppnår sitt maksimum og minimum
på
oppnår sitt maksimum og minimum
på 
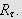 La oss si
La oss si

![]() oppnår sitt maksimum i et punkt
oppnår sitt maksimum i et punkt

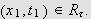 Dette maksimum er opplagt
Dette maksimum er opplagt

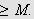 Da
må
Da
må 
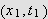 enten være et indre punkt i
enten være et indre punkt i

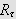 eller
eller

 Punktet
Punktet

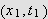 kan ikke ligge på randen
kan ikke ligge på randen

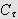 for der har vi for alle
for der har vi for alle

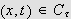 at
at
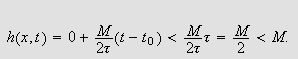
(i) Hvis

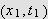 er et indre punkt i
er et indre punkt i

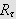 vet vi fra flerdimensjonal analyse at
vet vi fra flerdimensjonal analyse at
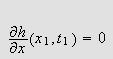
og
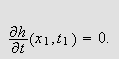
Dessuten
må
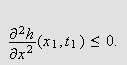
(ii) Hvis i stedet

 så må vi ha
så må vi ha
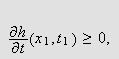
siden

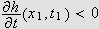 ville gitt at det fantes
ville gitt at det fantes

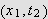 med
med

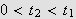 s.a.
s.a.
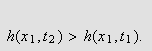
Vi befinner oss nå på øverste kant av

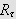 og fra vanlig envariabelteori må vi da
ha
og fra vanlig envariabelteori må vi da
ha
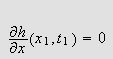
og
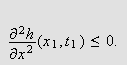
Sammenlikner vi (i) og (ii) ser vi at vi har
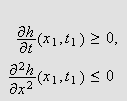
i begge tilfeller. Siden
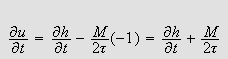
blir
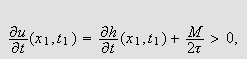
mens
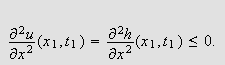
Innsatt i varmelikningen () kan vi da se at
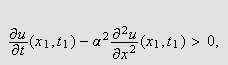
og vi har en selvmotsigelse, siden () da ikke vil væ re oppfyllt.
Altså må antakelsen være feil, og vi kan konkludere med at

![]() virkelig oppnår sitt maksimum
på
virkelig oppnår sitt maksimum
på 
 Det samme resonnementet vil gi at
Det samme resonnementet vil gi at

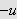 oppnår sitt maksimum, som er det samme som å si at
oppnår sitt maksimum, som er det samme som å si at

![]() oppnår sitt minimum
på
oppnår sitt minimum
på 
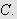
Vi kan da vise entydigheten til løsningen av varmelikningen.
La

![]() og
og

![]() være kontinuerlige løsninger av (), der
være kontinuerlige løsninger av (), der

![]() og
og

![]() Da er
Da er

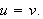
Sett

![]() Dette er en lineærkombinasjon av løsninger, og
Dette er en lineærkombinasjon av løsninger, og

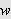 vil da også være en løsning av varmelikningen. Dessuten vil
vil da også være en løsning av varmelikningen. Dessuten vil

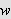 tilfredsstille
tilfredsstille

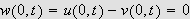 og
og

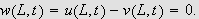 Siden
Siden

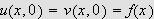 har vi
har vi

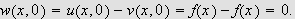 Altså har vi at
Altså har vi at

![]() på
på 
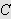 ,
og lemma 3 gir da for
,
og lemma 3 gir da for

![]() at
at
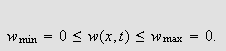
Dette viser oss at

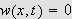 og dermed er
og dermed er
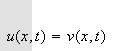
for alle

![]()
| [JF] | Fourier, J.: Analytical theory of heat |
| Dover publications (1955) | |
| [B/DiP] | Boyce, W.E./DiPrima, R.C.: Elem. diff. equations and boundary value problems |
| John Wiley & sons, Inc. (1992); ISBN: 0-471-57019-2 | |
| [TL1] | Lindstrøm, T.: Kalkulus |
| Universitetsforlaget AS (1995); ISBN: 82-00-22472-4 | |
| [PRA] | Andenæs, P.R.: MNFMA219 - Reell analyse |
| NTNU (2000) | |
| [E/P] | Edwards, C.H../Penney, D.E.: Calculus with analytic geometry |
| Prentice Hall Inc. (1994); ISBN: 0-13-176728-3 |
Neste: Problemene This document created by Scientific WorkPlace 4.0.
Forrige: Bakgrunn